Question 1033062: On the Fahrenheit scale for measuring temperature, 32 degrees is the freezing point of water, and 212 degrees is the boiling point. Michael invented his own temperature scale, which also is linear, where water freezes at 83 degrees and boils at 128 degrees. If the temperature is 98 degrees on Michael's scale, what is the temperature in degrees Fahrenheit? At what temperature are the two scales the same?
SO far, I've tried to use ratios to answer this question, but the difference or the values are different, so it doesn't make sense.
Found 2 solutions by josgarithmetic, solver91311:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! The relationship between the scales is a little beyond just ratio. It is relating two ordered pair.
Fahrenheit Michael DATA POINT, (F,M)
FREEZE 32 83 (32,83)
BOIL 212 128 (212,128)
Find the equation for the LINE which has the two points.
You can use the point-slope form and first find the slope between the two points.
 , understand that , understand that 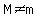 ; ;


-
 as the point-slope form equation; as the point-slope form equation;
M..... BUT notice the question: What is the FAHRENHEIT TEMPERATURE FOR 98 DEGREE ON THE M SCALE?
-
Solve the equation for F in terms of M.



 , formula to convert from M to F degree temperature. , formula to convert from M to F degree temperature.
The QUESTION:
M=98; find F.


--
You could avoid finding the linear equation and chose to perform linear interpolation instead. Either way accomplishes the same thing; that of finding a coordinate intermediate between two other coordinates. (92,98) is just another point on the line.
--
FURTHER DISCUSSION
The two points are part of a line which defines how to relate the two temperature scales. The line will be the set of ordered pairs, (T, M).
You want to find the slope of the two points, and choose either data pair in order to find the equation for the line.
Let m be the slope of the line.

which can be symbolized using the variable names in use in this example, as  . .
DO NOT CONFUSE THE lower case and upper case variable naming! I am using m for slope and M for temperature value on Michael scale.
The slope formula as shown here can be rearranged, by MULTIPLYING the left and right members by 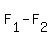 . .


and understand that one of your points will be known and both given points would allow the slope m to be calculated or computed. Let therefore (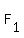 , ,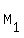 ) be any variable point (F,M). Use these in place of the "sub one" variable in the form. ) be any variable point (F,M). Use these in place of the "sub one" variable in the form.
That would be  , ,
but you could certainly choose "sub one" data point if you want to.
This is the POINT-SLOPE FORM EQUATION FOR A LINE, using independent variable F and dependent variable M.
You can algebraically rearrange the formula to solve F in terms of M if you want.
Answer by solver91311(24713)   (Show Source): (Show Source):
|
|
|