Question 1032916: Please help me with this problem:
Suppose f(x) =  . Find the slope of the line which passes through the points(0,f(0)) and (2,f(2)). Illustrate the mean value theorem for derivatives by finding a number c in (0,2) such that f'(c) equals the slope of the line described.
Found 2 solutions by robertb, Edwin McCravy:
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! The two points are (0,2) and (2,6). The slope of the line passing through them is  .
f'(x) = 2x.
Since f(x) is differentiable on the interval (0,2) and continuous on the interval [0,2], there is a c in the interval (0,2) such that f'(c) =  .
Indeed, 2c = 2 ==> c = 1.
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
We draw the graph of f(x) = x²+2.
We find f(0) = 0²+2 = 2 and f(2) = 2²+2 = 6
Then the points (0,f(0)) and (2,f(2)) are (0,2) and (2,6),
We plot those and draw a line through them
(the green line below):
Next we find the slope of that green line, using the
slope formula from algebra:
m = 
where (x1,y1) = (0,2)
and where (x2,y2) = (2,6)
m = 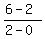 =  = 2
Now we want to find a point on the graph, between those
two points where the slope of a tangent line is parallel
to the green line.
The derivative is a formula for the slope of the tangent
line at any point we substitute the x-coordinate in.
f(x) = x²+2
f'(x) = 2x
We set 2x equal to the slope 2 of that green line.
2x = 2
x = 1
That means that at the point (1,f(1)) which is (1,1²+2)
or (1,3), if we draw a line tangent to the graph at that
point it will be parallel to the green line. So we draw
a tangent line at the point (1,3) (in blue), and we notice
that it is parallel to the green line:
I have drawn a black line from the point of tangency
of the blue line down to the x-axis to show that the value of
c on the x-axis in the interval (0,2) is the value c=1.
What this is all about is showing you that if you have a
line that cuts a curve in two points there is always a point
between them where you can draw a tangent line paralell to
that line that cuts through the curve. Then the x-coordinate
of that point of tangency is the value of c.
Edwin
|
|
|
