SOLUTION: List all elements of the set A ∩ B, where A = {n ∈ N | ∃k ∈ N such that n = 2^k + 2}, B = {n ∈ N | ∃k ∈ N such that n = 2^k − 2}.

Algebra ->  Test -> SOLUTION: List all elements of the set A ∩ B, where A = {n ∈ N | ∃k ∈ N such that n = 2^k + 2}, B = {n ∈ N | ∃k ∈ N such that n = 2^k − 2}.      Log On


   

Question 1023501: List all elements of the set A ∩ B, where
A = {n ∈ N | ∃k ∈ N such that n = 2^k + 2},
B = {n ∈ N | ∃k ∈ N such that n = 2^k − 2}.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
The first few elements of A are
2%5E0%2B2+=+3, 2%5E1%2B2+=+4, 2%5E2%2B2+=+6, 2%5E3%2B2+=+10, 2%5E4%2B2+=+18, 2%5E5%2B2+=+34,...
The first few elements of B are
2%5E1-2=+0, 2%5E2-2+=+2, 2%5E3-2+=+6, 2%5E4-2+=+14, 2%5E5-2+=+30,...
It is quite clear that 6 is a common element, so 6 is in A ∩ B.
Now we show that for k and l%3E=4, there are no other common terms.
Suppose there are, or suppose there are natural numbers a, b%3E=4 such that
2%5Ea+%2B+2+=+2%5Eb+-+2
==> 2%5Ea+%2B+4+=+2%5Eb,
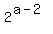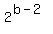==> 2%5E%28a-2%29%2B1++=+2%5E%28b-2%29, contradiction, because 2%5E%28a-2%29 and 2%5E%28b-2%29 would both be even since a, b%3E=4.
Therefore A ∩ B = {6}.