Question 1015468: I am in straight panic mode and can't figure this out
The following amounts represent the costs for producing a particular item. Assume the cost function for producing x items is linear. Find the cost function, revenue function, and profit function.
Fixed Cost Marginal Cost Per Item Item Sells For
15,000 8.50 45
What is the cost function C(x)=
What is the revenue function R(x)=
What is the profit function? P(x)=
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! fixed cost is 15,000
marginal cost per item is 8.50
sale price per item is 45.
marginal cost per item appears to me to be the cost per item above and beyond your fixed cost.
it more than likely includes material plus labor.
the fixed cost more then likely includes the cost of the machine that produces the item.
there are also other fixed costs involved such as land and building that are probably not included in this.
no matter.
the formulas would be as follows:
c(x) = fc + vc
fc is fixed cost
vc is cost per item sold.
that's what is called your marginal cost.
r(x) = vr
vr is revenue per item sold.
p(x) = r(x) - c(x)
this tells you that your profit is equal to your revenue minus your cost.
in your problem:
fc = 15,000
vc = 8.50
rc = 45.00
your cost formula becomes:
c(x) = 15,000 + 8.50 * x
your revenue formula becomes:
r(x) = 45 * x
your profit formula becomes:
p(x) = r(x) - c(x) = 45 * x - (15,000 + 8.50 * x)
simplify this to get p(x) = 45 * x - 15,000 - 8.50 * x
simplify further to get p(x) = 36.5 * x - 15,000.
so you have:
c(x) = 15,000 + 8.50 * x
r(x) = 45 * x
p(x) = r(x) - c(x) = 36.5 * x - 15,000
your break even point is when r(x) = c(x).
set c(x) = r(x) and the formula becomes:
15,000 + 8.50 * x = 45 * x
subtract 8.50 * x from this both sides of this equation and you get:
15,000 = 45 * x - 8.50 * x
simplify to get 15,000 = 36.5 * x.
divide both sides of this equation by 36.5 to get x = 410.9589041.
if you sell 410.9589041 items, you will break even.
45 * 410.9589041 = 18,493.15068 in revenue.
your cost was 15,000 + 8.5 * 410.9589041 = 18493.15068.
when you broke even, your profit was 0.
p(x) = r(x) - c(x) = 0
p(x) = 36.5 * x - 15,000
when x = 410.9589041, p(x) becomes 36.5 * 410.9589041 - 15,000 = 0
do the math and you get 0 = 0 which confirms the equation is true.
you can also graph these equations.
the equations to graph are:
r(x) = 45 * x
c(x) = 15,000 + 8.5 * x
p(x) = 36.5 * x - 15,000
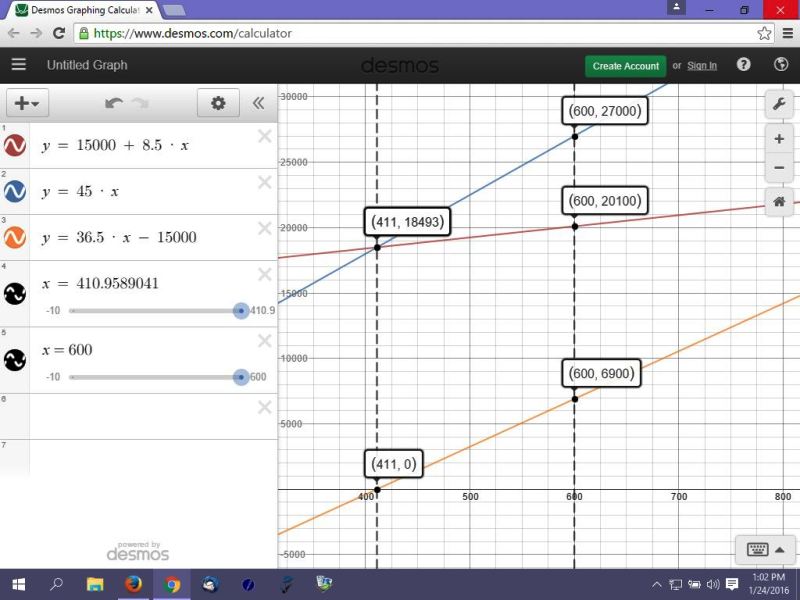
your graph is shown below.
the red line is the graph of your cost equation.
the blue line is the graph of your revenue equation.
the orange line is the graph of your profit equation.
you break even when your cost is equal to your revenue.
that happens when the number of items you sell is 410.9589041.
that's the intersection of your cost line and your revenue line on the graph.
since you can't sell 410.9958... items, your break even point is between when you sell 410 items and when you sell 411 items.
your profit when you break even is equal to 0.
that's shown on the graph of your profit equation.
profit is equal to revenue - cost.
at break even, your revenue and your cost are equal so your profit is equal to 0.
when you sell 600 items, your profit is 6900.
profit = revenue minus cost.
when you sell 600 items, your revenue is 27000 and your cost is 20100.
27000 - 20100 = 6900.
the graph is showing you what the equations are telling you.
|
|
|