SOLUTION: If a,b,c are in G.P. Then prove that (a^2+ab+b^2)/(bc+ca+ab)=(b+a)/(c+b)

We are given that a,b,c are in G.P.  Therefore:



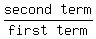
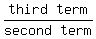or



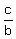or upon cross-multiplying:

(1)   

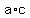When the conclusion is more complicated than the premise,
the best plan is to do an INDIRECT proof.  We will begin
by assuming the premise true, that is, that a,b,c are in 
G.P., but that the conclusion: 



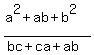
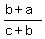is false. 

That is we start by assuming the conclusion is false, i.e., that:



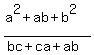
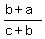Let's use (1) above to substitute ac for b2 in the numerator,
and b2 for ca, which is the same as ac,  in the denominator
on the left:



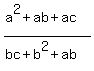
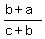Factor a out of the numerator and b out of the denominator:



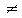
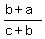We can cancel (a+b+c) and (c+b+a) on the left and get



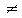
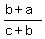The inequality will still hold if we cross-multiply:



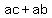
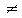
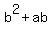The inequality will still hold if we subtract ab from both
sides:



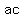
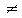
This contradicts (1).

Therefore the assumption 



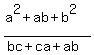
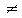
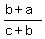is false and therefore:



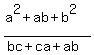
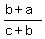Edwin