Question 994509: Why is the product of a non zero rational number and an irrational number irrational ?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
"The product of a non-zero rational number and an irrational number is irrational."
Indirect Proof (Proof by Contradiction) of the statement:
Assume the opposite of what you want to prove, and show it leads to a contradiction of a known fact.
assume  is an irrational number, and the product of is an irrational number, and the product of  and a rational and a rational  is rational is rational  , where , where  , , , , , and , and  are integers ( are integers (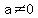 , ,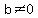 , , ). ).
Then  . .
By division,  => => . .
Since integers are closed under multiplication, 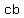 and and  are integers, making are integers, making  a rational number by definition. This is a contradiction to the given fact that a rational number by definition. This is a contradiction to the given fact that  is an irrational number. The assumption is wrong. The product of a non-zero rational number and an irrational number is an irrational number. is an irrational number. The assumption is wrong. The product of a non-zero rational number and an irrational number is an irrational number.
|
|
|