Question 970091: A function is shown below:
f(x) = x3 + 3x2 - x - 3
Part A: What are the factors of f(x)? Show your work.
Part B: What are the zeros of f(x)? Show your work.
Part C: What are the steps you would follow to graph f(x)? Describe the end behavior of the graph of f(x).
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! The potential factors of x^3-3x^2-x-3 are +/- 3 and +/- 1; I need 3 roots or 2 roots with one a square.
Trying -3 (factor x+3)
-3 1 ; 3 ;-1 ;;-3
;;; 1; -3;; 0 ;; 3 (+3) (difficult to format synthetic division)
;;;;;;;;0;; -1;;0
This works with no remainder, so (x+3) and (x^2-1) are factors.
Difference of squares noted:
Factors are (x+3) (x+1) (x-1)
Each of those =0 will give me zeros.
-3, -1, 1
For -3: -27 +27 +3 -3 =0
For 1: 1+3-1-3=0
For -1: -1+3 +1 -3=0
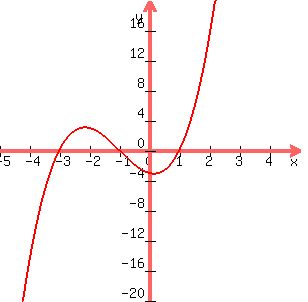
To graph it
y=a (x+3) (x-1)(x+1)
point (0,-3) is on the graph (the constant).
-3= a (3)(-1) (1)
a=1
y=(x+3)(x+1)(x-1)
To the left of minus 3, the graph goes negative, driven by the first negative cubic term.
It rises through the root -1 and drops to 0,-3, when x=0. It then rises for good, passing through (1,0) and becoming driven by the positive cube.
|
|
|