Question 890619: A tiled floor of a room has a dimension m*m sq-m dimensions of tile used are n*n sq-m. All tiles used are green tiles except diagonal tiles are red. After some years some green tiles are replaced by red tiles to form alternate red and green tiles pattern how many green tiles are removed? (m not equal to n)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the floor is completely covered with the tiles, then 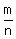 is a positive integer. is a positive integer.
That is the number of tiles along each side of the square room,
and it is also the number of tiles in the diagonal.
The total number of tiles is 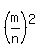 . .
If 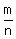 is even, in an alternating pattern, half of the tiles would be red. is even, in an alternating pattern, half of the tiles would be red.
The final number of red tiles would be
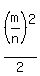
The number of green tiles replaced (the number of red tiles added) would be

If 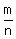 is an odd number, an alternating pattern with a red diagonal would have is an odd number, an alternating pattern with a red diagonal would have
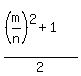 red tiles and red tiles and 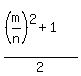 green tiles. green tiles.
The number of green tiles to be replaced (the number of red tiles to be added) would be

UNFORTUNATELY, there is no simple formula that covers both cases (when 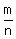 is even, and when is even, and when 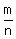 is odd). is odd).
If you want a single formula, I would have to write something complicated, like
 or or 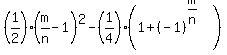
For  , which is odd, we are replacing , which is odd, we are replacing
 tiles, or tiles, or
 tiles, or tiles, or
 tiles. tiles.
 The new (replacement) red tiles are the ones in the green triangles. The new (replacement) red tiles are the ones in the green triangles.
There are  in each triangle. in each triangle.
|
|
|