Question 704297: how can i understand foiling and factoring better?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Factoring takes practice and it is hard work.
The good news is that factoring gets easier with practice, and it is a very efficient way to solve some quadratic equations.
The bad news is that factoring keeps coming up in math, from rational functions and quadratic equations all the way to calculus.
I will show you my strategies, along with the rationale behind it.
Understanding the rationale helps me remember procedures without having to memorize "recipes" that make no sense to me.
There will be too many words, but I'll use more pictures as it gets too complicated for just words..
I assume you know that the first thing to do when factoring a complicated expression is to look for common factors.
If you have a polynomial like 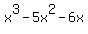 , with , with  in all the terms, in all the terms,
you would first "take out the common factor"  , as in , as in

FOIL is an acronym teachers use to help you remember all the terms when multiplying two binomials.
When multiplying the binomials 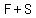 times times 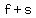
you get a sum of all four possible products:

In the acronym FOIL,
F stand for First terms multiplied make 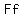
O stands for Outside terms multiplied make 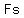
I L stands for stands for Inside terms multiplied make 
Last term multiplied make 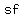
Thinking of FOIL makes sure you include all four products, just once each, and nothing else.
In 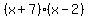 , the first , the first  and and  are the Outside terms. are the Outside terms.
The  and the and the  that appear together in the middle are the Inside terms that appear together in the middle are the Inside terms
 is the First terms multiplied, is the First terms multiplied,
 is the Outside terms multiplied, is the Outside terms multiplied,
 is the Inside terms multiplied is the Inside terms multiplied
After the "foiling" often comes the "collecting like terms", so after

you add together the terms in  , ,  and and  to get to get

and then you have

Factoring  is "unfoiling". is "unfoiling".
You know that the  is the product of two first terms that must have been is the product of two first terms that must have been  in both binomials. in both binomials.
You know that the  term is the product of two last terms, and it is not that clear what those two last terms were. term is the product of two last terms, and it is not that clear what those two last terms were.
There are several possibilities (four to be specific):
   and and 
In the foiling, the last terms of the binomial were also used as factors in the Outside and Inside products to make two terms in  . .
In those two terms in  the last terms of the binomial appeared as coefficients in front of x. the last terms of the binomial appeared as coefficients in front of x.
The problem is that the two terms in  from the foiling were already "collected" together into the from the foiling were already "collected" together into the 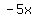 term, term,
so the coefficients were added together to get  . .
We go back to the four possibilities and see what pair adds up to  : :
   and and 
so the two last terms must be 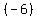 and and 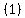 . .
So the factoring is

A PICTURE:
In the picture below, the large square represents the product  . .
It is what happens when a patio  tiles long by tiles long by  tiles wide tiles wide
is enlarged by adding  rows of tiles to the length and rows of tiles to the length and  rows to the wdith. rows to the wdith.
 Foiling is multiplying the side measures to get the area of the rectangle. Foiling is multiplying the side measures to get the area of the rectangle.
The figure below illustrates 

Factoring is figuring out the rectangle sides from the area.
The figures below illustrates factoring 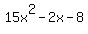
I will pretend that I do not know what the factors were as I try to undo the multiplication.
 If you multiply together opposite corners, you find that they are the same. If you multiply together opposite corners, you find that they are the same.
 and and 
so the 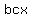 and and 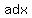 that we are looking for must be factors of that we are looking for must be factors of

We look for pairs of factors that multiply to  without worrying much about signs, or about the without worrying much about signs, or about the  . .
I know that 1,2,3,4,5,6,8,10,and 12 are factors because they divide 120 evenly).
Dividing 120 by each of the small,easy to find factors, I find the matching larger factors.

When I get to  I realize that I realize that 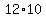 involves the same pair of factors I had already found as involves the same pair of factors I had already found as 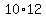 , so I know I have found all the factors. , so I know I have found all the factors.
Because the product has a minus sign, I know that one of the factors must have a minus sign.
Because they must add to the  in in  , I figure that I am looking for a pair of factors that differ by , I figure that I am looking for a pair of factors that differ by  and I am going to give the minus sign to the larger factor. and I am going to give the minus sign to the larger factor.
 is the answer is the answer
 does not work, and neither do the other pairs. does not work, and neither do the other pairs.
 and and  are the coefficients I am looking for. are the coefficients I am looking for.
I fill the 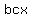 and and 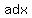 squares with squares with 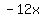 and and  . .
It does not matter where I put each one.

Now I need to figure common factors for each row and column. Those common factors will replace the question marks.
I start with what seems more obvious to me, whatever I can figure out faster.
The  and and  in the left column share in the left column share  as a common factor, so I put it above the left column. as a common factor, so I put it above the left column.
The  and and 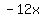 in the top row share in the top row share  as a common factor, so I put it to the left of the top row. I could also have figured it, from what I already knew, as as a common factor, so I put it to the left of the top row. I could also have figured it, from what I already knew, as
 . .
The other question marks, I can figure out from what I already know:
 goes above goes above 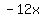 and and
 goes above goes above  . .

SPECIAL PRODUCTS:
There are special products that you end up remembering after a while, and are represented by the "formulas" below.
Square of a binomial:

Difference of squares:

That one is easy to explain because when you FOIL, the O and I products cancel out, so your FOIL turns into FL (I cal that Florida).
Difference of cubes:

Sum of cubes:

|
|
|