Question 650112: Explain and demonstrate how to factor a trinomial in the form: ax^2+bx+c with an example where a, b and c are values
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
what you are looking for is called 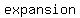 and and 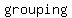
so, you have to to expand "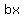 " into " into  terms, such that one term will have a terms, such that one term will have a   with with  and the other will have a and the other will have a   with with 
for example:
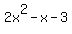
you are going find numbers that are factors of  (these are (these are 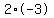 ) ) that ) ) that 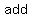  to to  ( ( ) )
these factors are  and and 
so you would rewrite the equation as:
 (doing so,you didn't really change anything, because (doing so,you didn't really change anything, because  , so the integrity of the expression is still there) , so the integrity of the expression is still there)
now you factor in parts. from the first part, take out  , from the second, take out , from the second, take out 
so, you have:
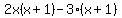 . . . . (if you notice, both of the terms in the ()'s are the same, this will always happen if it doesn't, you have done something wrong . . . . (if you notice, both of the terms in the ()'s are the same, this will always happen if it doesn't, you have done something wrong
then you say:
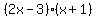 ...that's factored ...that's factored
if u multiply this out, you will get back to the original expression of 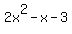
|
|
|