Question 599636: How do you solve problems that have an exponent to the left of a radical?
___
For example: ^3 \| 343
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Your example is the way you write cube roots, meaning that it tells you to find a number that when multiplied by itself three times results in a product of 343.
.
It is written as:
.
.
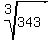
How can you determine what the answer to your example should be? Here are some ways to think about this problem:
.
First, you know that 10 times 10 times 10 equals 1000. This tells us that the answer has to be less than 10 because we need a product of 343, and the product of 1000 is way too big.
.
Second, in your head you can multiply 5 times 5 times 5 to get a product of 125. This tells us that 5 is too small because we need a product that is 343, and the product of 125 is too small.
.
So far we have narrowed down the possible answers. They are between 5 and 10.
.
Now recognize the fact that the answer must be an odd number. Why??? Because when you multiply an even number times itself three times, you will always get a product that is even. But the product that we are looking for, namely 343, is an odd number. So the answer can't be an even number. We need an odd number that is bigger than 5 but less than 10. There are only two odd numbers between 5 and 10 and they are 7 and 9.
.
9 times 9 is 81 and then multiplying 81 times the third 9 results in a number that is over 700. That product is too big.
.
Finally, let's try 7 times 7 times 7. The first part 7 times 7 is 49 and then we multiply 49 times the third 7 and the result is 343 ... the answer we were looking for. So we can write the equation:
.
.
In general, what you called the "exponent" is not really an exponent. That number tells you what root you are looking for, the root being the number of times that you multiply the answer by itself to get the number inside the radical symbol. The single exception to this is for the square root which is not written as having an "exponent" of 2. It is just understood that a radical symbol without the "exponent" as you called it means find the square root, a number that when multiplied by itself results in the product of the number inside the radical symbol.
.
In summary we can write that if you are given a number x, its:
.
square root y is given by  meaning y * y = x
.
cube root y is given by  meaning y*y*y = x
.
fourth root y is given by  meaning y*y*y*y = x
.
fifth root y is given by  meaning y*y*y*y*y = x
.
sixth root y is given by  meaning y*y*y*y*y*y = x
.
and so on.
.
I hope this helps you to understand the method of writing roots and what they mean.
.
|
|
|
