SOLUTION: Find the greatest power of 98,which can divide 99! -98!.answer choices 10,9,8,14.

Algebra ->  Test  -> Lessons -> SOLUTION: Find the greatest power of 98,which can divide 99! -98!.answer choices 10,9,8,14.      Log On


   

Question 550232: Find the greatest power of 98,which can divide 99! -98!.answer choices 10,9,8,14.
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
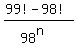%2899%21-98%21%29%2F%2898%5En%29 =
 
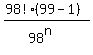%2898%21%2899-1%29%29%2F%2898%5En%29 =
 
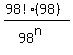%2898%21%2898%29%29%2F%2898%5En%29 =
 
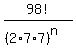98%21%2F%28%282%2A7%2A7%29%5En%29 =

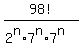98%21%2F%28++2%5En%2A7%5En%2A7%5En++%29 =

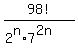98%21%2F%28++2%5En%2A7%5E%282n%29++%29 =


The denominator must cancel entirely into the numerator.  If we have enough
factors which are multiples of 7's in the denominator to cancel entirely into
the multiples of 7's which are factors of the numerator, then we will
automatically have enough factors of multiples of 2 since there are fewer
multiples of 2 in the denominator than multiples of 7 and there are 48 even
factors in the top, so we only need be sure there are as many factors which are
multiples of 7 in the denominator to cancel into the 16 multiples of 7 in the
numerator.  How did I know there were 16 multiples of 7 which are factors of
the numerator?  Here's how I knew. The integers from 1 to 98, inclusive are
factors of the numerator of 98!, there are 14 which are multiples of 7.  There
are 98÷7 or 14 multiples of 7.  These are:
7,14,21,28,35,42,49,56,63,70,77,84,91,98.  Each of those has 7 as a factor
once, except 49 and 98 which each have a factor of 7 twice.  So that makes 16
factors of 7 in the numerator. 

So the 2n 7's in the bottom must cancel completely into the the 16 multiples of
7 in the top.  So

    2n ≤ 16
     n ≤ 8
    
So 8 is the biggest possible value of n.

Edwin