I will put  on the limits to show what variable the
limits are on, namely x, since we will be changing the limits:
on the limits to show what variable the
limits are on, namely x, since we will be changing the limits:
 Let
Let  Then
Then  or
or  and
and  So we substitute
So we substitute  for
for 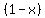 and
and  for
for 
 And we can take out the negative sign in front of the integral:
And we can take out the negative sign in front of the integral:
 But the limits are on x. We want to change the limits
so that they will be on u rather than x.
To do that we substitute the limits for x in the equation
for u which is
But the limits are on x. We want to change the limits
so that they will be on u rather than x.
To do that we substitute the limits for x in the equation
for u which is  when
when  ,
,  and
when
and
when  ,
,  ,
so we change the limits to:
,
so we change the limits to:
 and we use the power formula
and we use the power formula 
 Edwin
Edwin