Question 204562: Hi there, I have an exam today and I was doing a practise exam where I came across this Polynomial and rational functions question and was unable to solve it. Could one of the tutors please help me with it, I'd be more than grateful!!!!
Find the remainder:(x^4 - 2x^2 + 5 - 2)/(x - 3). (2 marks)
Answer by mickclns(59)   (Show Source):
You can put this solution on YOUR website! Did you forget the x after the 5? I am assuming you did, so we have:
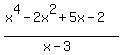
You could use long (polynomial) division, but since the divisor is linear, synthetic division is easier:
The 3 at upper left is the root of x-3, the linear divisor.
The 1 to its right is the coefficient of  .
As we move to the right we have the rest of the coefficients, 0, -2, 5, -2, including the (necessary) 0 for the non-existent  term.
The first coefficient, 1 in this case, we always bring straight down and put below the (long) horizontal line. Then we multiply that 1 by the 3 and put the resulting 3 in the second row, second column. Next, we add THAT 3 to the 0 above it and put the resulting 3 below the line. That 3 gets multiplied by the original 3 (root of x-3) and the resulting 9 in the second row, third column.
Then repeat: 9 + -2 is 7, 7 x 3 is 21, 21 + 5 is 26, 26 x 3 is 78, 78 + -2 is 76, which is where we stop because we have no more columns. The bottom right number is our remainder and is separated from the others by lines for that reason.
Three things to notice about this result:
1) if it is 0, then the denominator divides the numerator in the original fraction evenly.
2) the remainder is also what you get when you plug the top right number into the numerator. In other words, in this case,  . This is usually a much easier process than taking 3 to the 4th power, subtracting from it ... . When used in this way it is called synthetic substitution.
3) Look back at the diagram. This shows that  , which is also what would have resulted from using long division.
|
|
|
