Question 1210371: Candidates Q, R, and T are allowed to solve an advanced level Physics question independently. The probability that Q solves the question is 9/10, R solves the question is 3/7, and T solves the question is x.
(a) If the probability that at least one candidate solves the question is 19/70, find the value of x.
(b) Find the probability that:
(i) At least one candidate solves the question.
(ii) At most one candidate solves the question.
Found 4 solutions by math_tutor2020, ikleyn, mccravyedwin, Edwin McCravy:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
Part (a)
P(Q) = probability that candidate Q solves the question
P(Q or R or T) = probability that at least one candidate solves the question
Use the inclusion-exclusion principle to say the following:
P(Q or R or T) = P(Q) + P(R) + P(T) - P(Q and R) - P(Q and T) - P(R and T) + P(Q and R and T)
P(Q or R or T) = P(Q) + P(R) + P(T) - P(Q)*P(R) - P(Q)*P(T) - P(R)*P(T) + P(Q)*P(R)*P(T)
P(Q or R or T) = 9/10 + 3/7 + x - (9/10)*(3/7) - (9/10)*x - (3/7)*x + (9/10)*(3/7)*x
P(Q or R or T) = (2x+33)/35
Set this equal to 19/70 and solve for x.
Doing so will lead to x = -47/4 = -11.75, but this is not a valid result since x must be in the interval from 0 to 1.
A probability of -11.75 makes no sense.
It appears some of the given probability values are flawed.
You'll need to contact your teacher for clarification.
Or perhaps there's something I might be overlooking.
Another way to arrive at this x value.
P(Q') = probability that Q fails to solve the question
P(Q') = 1 - P(Q) = 1 - 9/10
P(Q'R'T') = probability all 3 people fail
P(Q'R'T') = P(Q')*P(R')*P(T')
P(Q'R'T') = (1-9/10)*(1-3/7)*(1-x) = 1-19/70
(1-9/10)*(1-3/7)*(1-x) = 1-19/70
Solving that equation should lead you to x = -47/4 = -11.75
Notice that the events "at least one solves the question" and "all 3 fail to solve" are complementary events.
One or the other must happen.
This complementary nature is why we're allowed to subtract the probabilities from 1.
Answer by ikleyn(52754)  (Show Source):
You can put this solution on YOUR website! .
Candidates Q, R, and T are allowed to solve an advanced level Physics question independently.
The probability that Q solves the question is 9/10, R solves the question is 3/7, and T solves the question is x.
(a) If the probability that at least one candidate solves the question is 19/70, find the value of x.
(b) Find the probability that:
(i) At least one candidate solves the question.
(ii) At most one candidate solves the question.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
My dear visitor,
the problem in your post is posed INCORRECTLY.
Indeed, if the probability for Q to solve the problem is 9/10,
then the probability that "at least one candidate" will solve the problem
MUST BE AT LEAST 9/10.
But in your post the probability that at least one candidate will solve the problem is given as 19/70,
which makes no sense, contradicts to common sense and kills the problem to the death, instantly.
My condolences.
Answer by mccravyedwin(405)  (Show Source):
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
I'm thinking that you may have typed 19/70 when it should have been 69/70.
Candidates Q, R, and T are allowed to solve an advanced level Physics question
independently. The probability that Q solves the question is 9/10, R solves the
question is 3/7, and T solves the question is x.
(a) If the probability that at least one candidate solves the question is
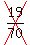  , find the value of x.
The probability that at least one candidate solved it is 1 minus the probability
that no candidate solved it, which is
    
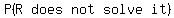
This must equal 1-69/70 or 1/70
 <-- the value of x, which is the probability that T solves it.
>>>(i) At least one candidate solves the question.
Now, I do have to wonder why you asked this, since you gave it as 19/70 and I
changed it to 69/70.
The answer, of course is 69/70. LOL
>>>(ii) At most one candidate solves the question.
That's the probability that exactly one solved it or exactly none solved it.
case Q R T
1 Y N N (9/10)(1-3/7)(1-3/4) = (9/10)(4/7)(1/4) = 9/70
2 N Y N (1-9/10)(3/7)(1-3/4) = (1/10)(3/7)(1/4) = 3/280
3 N N Y (1-9/10)(1-3/7)(3/4) = (1/10)(4/7)(3/4) = 3/70
4 N N N (1-9/10)(1-3/7)(1-3/4) = (1/10)(4/7)(1/4) = 1/70
Sum those 4 fractions and get 11/56.
Edwin
|
|
|
