Question 1210363: A cone has a radius of 10cm and slant height of 26cm. find the volume of the cone
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to find the volume of the cone:
**1. Understand the Formulas**
To find the volume of a cone, you need its radius ($r$) and its height ($h$). The formula for the volume of a cone is:
$V = \frac{1}{3} \pi r^2 h$
You are given the radius ($r = 15 \text{ cm}$) and the slant height ($l = 20 \text{ cm}$), but you need to find the height ($h$).
**2. Find the Height (h)**
The radius, height, and slant height of a cone form a right-angled triangle, with the slant height as the hypotenuse. We can use the Pythagorean theorem:
$r^2 + h^2 = l^2$
Substitute the given values:
$15^2 + h^2 = 20^2$
$225 + h^2 = 400$
$h^2 = 400 - 225$
$h^2 = 175$
$h = \sqrt{175}$
To simplify $\sqrt{175}$:
$175 = 25 \times 7$
$h = \sqrt{25 \times 7} = 5\sqrt{7} \text{ cm}$
**3. Calculate the Volume (V)**
Now that you have the height, plug the values of $r$ and $h$ into the volume formula:
$V = \frac{1}{3} \pi r^2 h$
$V = \frac{1}{3} \pi (15)^2 (5\sqrt{7})$
$V = \frac{1}{3} \pi (225) (5\sqrt{7})$
$V = 75 \pi (5\sqrt{7})$
$V = 375\sqrt{7}\pi \text{ cm}^3$
**4. Approximate the Value (Optional)**
If you need a numerical approximation, use $\pi \approx 3.14159$ and $\sqrt{7} \approx 2.64575$:
$V \approx 375 \times 2.64575 \times 3.14159$
$V \approx 992.15625 \times 3.14159$
$V \approx 3117.85 \text{ cm}^3$
The exact volume of the cone is $375\sqrt{7}\pi \text{ cm}^3$.
Approximately, the volume is $3117.85 \text{ cm}^3$.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
A cone has a radius of 10cm and slant height of 26cm. find the volume of the cone
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill, giving the answer 3117.85 cm^3, is incorrect.
Below is my correct solution.
The height of the cone is h =  =  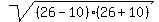=  = 4*6 = 24 cm to calculate it mentally.
The volume of the cone is V =  =  = 3.14159*100*8 = 2513.27 cm^3. ANSWER
Solved correctly.
===============================
The problem is elementary simple and routine, and my correct solution was in two lines.
The incorrect gibberish by @CPhill barely fit 30 lines.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solutions are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|
