SOLUTION: The dimensions of a square is given as 6.25 cm. A student measured one side of the square as 6.12 cm to calculate the perimeter and the area of the square. Find the percentag

Algebra ->  Test  -> Lessons -> SOLUTION: The dimensions of a square is given as 6.25 cm. A student measured one side of the square as 6.12 cm to calculate the perimeter and the area of the square. Find the percentag      Log On


   

Question 1210359: The dimensions of a square is given as 6.25 cm. A student measured one side of the square as 6.12 cm to calculate the perimeter and the area of the square.
Find the percentage error in:
i. Measured length
ii. Calculated perimeter
iii. Calculated area
Found 4 solutions by MathLover1, Edwin McCravy, ikleyn, mccravyedwin:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!


Find the percentage error in:
%

i. Measured length
%28%286.25-6.12%29%2F6.25%29%2A100%=2.08+%
the percentage error is 2.08%

ii. Calculated perimeter
4%2A6.25cm=25cm
4%2A6.12cm=24.48cm

%28%2825-24.48%29%2F25%29100%=2.08%

iii. Calculated area
6.25%2A6.25=39.0625
6.12%2A6.12=37.4544
%28%2839.0625-37.4544%29%2F39.0625%29100%=4.11674%


Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Although this problem can be solved exactly by algebra, as the other tutor has
solved it, I think this might be a calculus problem demonstrating using
differentials to approximate error.

>>The dimensions of a square is given as 6.25 cm. A student measured one side of
the square as 6.12 cm to calculate the perimeter and the area of the square.<<  
   
ds = 6.12 - 6.25 = -0.13
P = 4s
dP = 4ds = 4(-0.13) = -0.52
A = s2
dA = 2s(ds) = 2(6.25)(-0.13) = -1.625

>>Find the percentage error in:  
i. Measured length<< 
 
ds%2Fs+=-0.13%2F6.25+=+0.208+=+-%222.08%25%22
 
>>ii. Calculated perimeter<<

dP%2FP=%28-0.52%29%2F%284s%29=%28-0.52%29%2F%284%2A6.25%29=-0.0208=%22-2.08%25%22

>>iii. Calculated area<<  



Edwin

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
The dimensions of a square is given as 6.25 cm. A student measured one side of the square as 6.12 cm to calculate
the perimeter and the area of the square. Find the percentage error in:
i. Measured length
ii. Calculated perimeter
iii. Calculated area
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


        This problem is a standard 6-grade exercise for ratio and percentage.
        Therefore,  I solve it at the appropriate level using elementary algebra
        with complete explanations and without involving other approaches. 


In this problem, we are given the  precise value  of the side of the square as 6.25 cm,
and we also are given some measured value of the side of the square, 
which represents some deviation from the precise value.


For part (iii), we should calculate the deviation as the difference

    measured value  highlight%28highlight%28MINUS%29%29  the  precise value.    (1)


In this case, we have no measured value for the area, but we can compute it as the square
of the measured side,  6.12^2 cm^2.

So, doing it in the course of formula (1), we calculate the deviation of the computed area as

    computed area 6.12^2 cm^2 MINUS the precise area 6.25^2 cm^2,  or  6.12^2 - 6.25^2 = -1.6081 cm^2.


Then we relate this found deviation of the area to the EXACT GIVEN value of the area.
Doing this way, we obtain

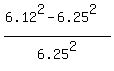    %286.12%5E2-6.25%5E2%29%2F6.25%5E2 = -0.04116736 = -0.041167  (rounded),  or -4.1167%.


The sign  " minus "  here points that the measured/computed area is less than the precise value.


But since the problem asks about the " error ", it instructs us to take the absolute value 
of the calculated "percentage of the deviation".


So, the correct answer for (iii) is 4.1167% (the positive value).

Solved.

------------------------------

Notice that in such problems,  choosing and using a correct treatment
is of a principial importance,  and it does not allow to split or to double or to modify the interpretation.

The whole wisdom in solving such problems is that if the precise value is given,
then we should calculate the percentage of the deviation using the formulas centered around this precise given value;
then we should take the absolute value for the final  " error value ".

Thus,  in accordance with the problem intention/purpose,  this my post  TEACHES  you
to interpret the problem correctly at the 6-grade level,  and also  TEACHES  you to choose and to use
ONE  single  UNIQUE  CORRECT  interpretation for this level
and work with it /(follow it)  it from the beginning to the end.



Answer by mccravyedwin(406) About Me  (Show Source):
You can put this solution on YOUR website!
In case you are studying what I think you are, and not a 6 grader, here are some
links:


Calculus - Differentials with Relative and Percent Error
https://www.youtube.com/watch?v=4DuQh5oUsbQ


Differentials: Propagated Error
https://www.youtube.com/watch?v=6u-ldWJKN7A

Edwin