Question 1210348: x, y, z ∈ Z³
13/x² + 1996/y² = z/1997
x, y, z = ?
Found 4 solutions by Edwin McCravy, mccravyedwin, ikleyn, AnlytcPhil:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Since 1996 is divisible by perfect squares 1 and 4, let
y2 = ± either of these.
Since 1996 is divisible by perfect squares 1 and 4, let
y2 = ± either of these.
 , and where y2 = 1 or 4 , and where y2 = 1 or 4


 For
For  , ,


 So that gives these solutions
(x,y,z) = (1,1,4011973), (1,-1,4011973), = (-1,1,4011973), = (-1,-1,4011973)
For
So that gives these solutions
(x,y,z) = (1,1,4011973), (1,-1,4011973), = (-1,1,4011973), = (-1,-1,4011973)
For  , ,


 So that gives these solutions
(x,y,z) = (1,2,2018967), (1,-2,2018967), = (-1,2,2018967), = (-1,-2,2018967)
in addition to these we already found:
(x,y,z) = (1,1,4011973), (1,-1,4011973), (-1,1,4011973), (-1,-1,4011973)
I doubt there are any other solutions besides these 8, but I don't know that for
sure.
Maybe another tutor can find others or show that there are no others.
Edwin
So that gives these solutions
(x,y,z) = (1,2,2018967), (1,-2,2018967), = (-1,2,2018967), = (-1,-2,2018967)
in addition to these we already found:
(x,y,z) = (1,1,4011973), (1,-1,4011973), (-1,1,4011973), (-1,-1,4011973)
I doubt there are any other solutions besides these 8, but I don't know that for
sure.
Maybe another tutor can find others or show that there are no others.
Edwin
Answer by mccravyedwin(406)   (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x, y, z ∈ Z³
13/x² + 1996/y² = z/1997
x, y, z = ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will list below two families of  solutions in solutions in  numbers (x,y,z). numbers (x,y,z).
(a) (x,y) = (+/-1, +/-1) ---> z = (13+1996)*1997 = 4011973. 4 solutions.
(b) (x,y) = (+/-1, +/-2) ---> z = (13+499)*1997 = 1022464. 4 solutions.
Why they are the solutions - it is obvious: it is enough to look at denominators.
I don't know if where are other solutions.
Edwin correctly recognized and pointed 4 solutions of family (a).
Edwin made an error pointing other 4 his solutions.
In my notations, they are 4 solutions (b), with (or after) my correction.
/////////////////////////////////////////////
Here is an addition to the set of solutions found by Edwin
(x,y,z) = (+/-7, +/-7, 81877).
Indeed, left side of the original equation is  + +  = =  = =  = 41, = 41,
and right side is 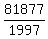 = 41. = 41.
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1210348
I kept on using the same technique, trying powers of 2 for x and y and
found all these solutions, and corrected the one I mis-punched my
calculator on.
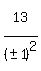  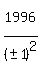  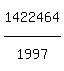   (x,y,z) = (1,1,1422464), (1,-1,1422464), (-1,1,1422464), (-1,-1,1422464).
These others give 4 solutions in the same way:
(x,y,z) = (1,1,1422464), (1,-1,1422464), (-1,1,1422464), (-1,-1,1422464).
These others give 4 solutions in the same way:
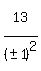  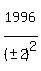      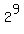
  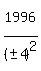      
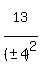  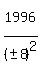      
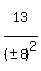        
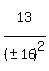    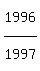    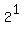 So, except for the 1st solution above, we could generalize on the others this
way. Maybe Ikleyn can prove this generalization for them:
So, except for the 1st solution above, we could generalize on the others this
way. Maybe Ikleyn can prove this generalization for them:
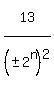    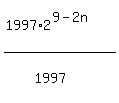  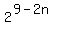 for n = 0,1,2,3,4
But I'm still not sure there are any other solutions. I said I was sure I had
all of them before, and then found these and had to eat my words. LOL
Edwin
for n = 0,1,2,3,4
But I'm still not sure there are any other solutions. I said I was sure I had
all of them before, and then found these and had to eat my words. LOL
Edwin
|
|
|