SOLUTION: A company installs solar panels in its premises to reduce its electricity cost. The monthly savings on electricity in $, is modelled by S=200+50x-2x², where x is the number of mon

The given quadratic function describes a parabola.


This parabola is opened downward, because the leading coefficient at  x^2  is negative.

So, the parabola has a maximum at its vertex.



(a)  the given quadratic function is increasing on the left of the vertex.

     x-coordinate of the vertex is  ,  where 'a' = -2 is the coefficient at x^2

     and 'b' = 50  is the coefficient at x.  So, x-coordinate of the vertex is  

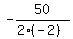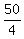                =  = 12.5.


     For the further analysis, take into account that 'x' in this problem is, factually, not a continuous time,
     but a discrete counter of months.  The value of 12.5 is exactly half-way between 12 and 13.
     Since the parabola is symmetric about the vertex coordinate, we round the time 12.5 months to 12 months.


     It means that the monthly saving on electricity stops increasing at the 12-th month, according to the given data.



(b)  To find the maximum monthly saving, calculate  the value of the given quadratic function at x = 12. 

     The maximum monthly saving will be   200 + 50*12 - 2*12^2 = 512 dollars.



Below is the table showing monthly savings for the first 15 months calculated using the given formula.

The table confirms that the monthly payment increases till the month 12 and stops increasing then.

It also confirms that the maximum monthly payment is $512.


month          monthly
               saving
------------------------
  1		248
  2		292
  3		332
  4		368
  5		400
  6		428
  7		452
  8		472
  9		488
 10		500
 11		508
 12		512
 13		512
 14		508
 15		500