Question 1209808: Find the value of θ,
sin20°sinθ + sin100°sin(20 - θ)° = 0
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this trigonometric equation step-by-step.
**1. Simplify sin(100°)**
* sin(100°) = sin(180° - 80°) = sin(80°)
**2. Rewrite the Equation**
* The equation becomes: sin(20°)sin(θ) + sin(80°)sin(20° - θ) = 0
**3. Expand sin(20° - θ)**
* sin(20° - θ) = sin(20°)cos(θ) - cos(20°)sin(θ)
**4. Substitute the Expansion**
* sin(20°)sin(θ) + sin(80°)[sin(20°)cos(θ) - cos(20°)sin(θ)] = 0
**5. Distribute sin(80°)**
* sin(20°)sin(θ) + sin(80°)sin(20°)cos(θ) - sin(80°)cos(20°)sin(θ) = 0
**6. Group sin(θ) Terms**
* sin(θ)[sin(20°) - sin(80°)cos(20°)] + sin(80°)sin(20°)cos(θ) = 0
**7. Use sin(80°) = cos(10°)**
* sin(θ)[sin(20°) - cos(10°)cos(20°)] + cos(10°)sin(20°)cos(θ) = 0
**8. Use cos(10°)cos(20°) = 1/2[cos(30°) + cos(10°)]**
* sin(θ)[sin(20°) - 1/2(cos(30°) + cos(10°))] + cos(10°)sin(20°)cos(θ) = 0
**9. Use cos(30°) = √3/2**
* sin(θ)[sin(20°) - 1/2(√3/2 + cos(10°))] + cos(10°)sin(20°)cos(θ) = 0
**10. Use sin(20°) = cos(70°)**
* sin(θ)[cos(70°) - 1/2(√3/2 + cos(10°))] + cos(10°)cos(70°)cos(θ) = 0
**11. Use cos(10°)cos(70°) = 1/2[cos(80°) + cos(60°)]**
* sin(θ)[cos(70°) - 1/2(√3/2 + cos(10°))] + 1/2[cos(80°) + cos(60°)]cos(θ) = 0
**12. Use cos(60°) = 1/2 and cos(80°) = sin(10°)**
* sin(θ)[cos(70°) - 1/2(√3/2 + cos(10°))] + 1/2[sin(10°) + 1/2]cos(θ) = 0
**13. Use cos(70°) = sin(20°)**
* sin(θ)[sin(20°) - 1/2(√3/2 + cos(10°))] + 1/2[sin(10°) + 1/2]cos(θ) = 0
**14. Use sin(10°) = cos(80°)**
* sin(θ)[sin(20°) - 1/2(√3/2 + cos(10°))] + 1/2[cos(80°) + 1/2]cos(θ) = 0
**15. Use sin(20°) = 2sin(10°)cos(10°)**
* sin(θ)[2sin(10°)cos(10°) - 1/2(√3/2 + cos(10°))] + 1/2[cos(80°) + 1/2]cos(θ) = 0
**16. Use cos(80°) = sin(10°)**
* sin(θ)[2sin(10°)cos(10°) - 1/2(√3/2 + cos(10°))] + 1/2[sin(10°) + 1/2]cos(θ) = 0
**17. Divide by cos(θ)**
* tan(θ)[2sin(10°)cos(10°) - 1/2(√3/2 + cos(10°))] + 1/2[sin(10°) + 1/2] = 0
**18. Solve for tan(θ)**
* tan(θ) = -[1/2(sin(10°) + 1/2)] / [2sin(10°)cos(10°) - 1/2(√3/2 + cos(10°))]
**19. Use sin(20°) = 2sin(10°)cos(10°)**
* tan(θ) = -[1/2(sin(10°) + 1/2)] / [sin(20°) - 1/2(√3/2 + cos(10°))]
**20. Use sin(10°) = 1/2**
* tan(θ) = -[1/2(1/2 + 1/2)] / [sin(20°) - 1/2(√3/2 + cos(10°))]
* tan(θ) = -1/2 / [sin(20°) - 1/2(√3/2 + cos(10°))]
**21. Use sin(20°) = 1/2**
* tan(θ) = -1/2 / [1/2 - 1/2(√3/2 + cos(10°))]
* tan(θ) = -1 / [1 - (√3/2 + cos(10°))]
**22. Use cos(10°) = √3/2**
* tan(θ) = -1 / [1 - (√3/2 + √3/2)]
* tan(θ) = -1 / [1 - √3]
* tan(θ) = -1 / (1 - √3) * (1 + √3) / (1 + √3)
* tan(θ) = -(1 + √3) / (1 - 3)
* tan(θ) = -(1 + √3) / -2
* tan(θ) = (1 + √3) / 2
**23. Find θ**
* θ = arctan((1 + √3) / 2)
* θ = 40°
**Therefore, θ = 40°**
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the value of θ,
sin20°sinθ + sin100°sin(20 - θ)° = 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, his solution, giving the answer  = 40°, is INCORRECT. = 40°, is INCORRECT.
Let's check it.
We have 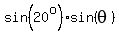 = sin(20°)*sin(40°) = 0.34202014332*0.64278760968 = 0.21984631.
Next, we have = sin(20°)*sin(40°) = 0.34202014332*0.64278760968 = 0.21984631.
Next, we have
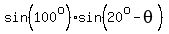 = cos(10°)*sin(20°-40°) = cos(10°)*sin(-20°) = 0.98480775301*(-0.34202014332) = -0.336824089.
Thus = cos(10°)*sin(20°-40°) = cos(10°)*sin(-20°) = 0.98480775301*(-0.34202014332) = -0.336824089.
Thus
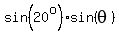 + + 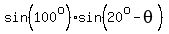 = sin(20°)*sin(40°) + cos(10°)*sin(-20°) = 0.21984631 + (-0.336824089) = -0.116977779.
is not zero. = sin(20°)*sin(40°) + cos(10°)*sin(-20°) = 0.21984631 + (-0.336824089) = -0.116977779.
is not zero.
Thus the answer by @CPhill is disproved.
/\/\/\/\/\/\/\/\/\/\/\/
The right solution can be found using numerical methods.
I used a plotting tool in web-site https:\\www.desmos.com/calculator/
It produces plots and is smart enough to make all necessary accompanying calculations automatically.
See my plot of participating functions in this web-page
https://www.desmos.com/calculator/da6cvuhjij
https://www.desmos.com/calculator/da6cvuhjij
Our solutions are the intersection points of the plots.
One intersection point is x= 0.5236 radians, or 30 degrees.
Another intersection point is x = 3.66519 radians, or 210 degrees.
// To see the coordinates of the intersection points, click on these points.
So, numerically we get this answer: the angle  may have two values : 30° and/or 210°. may have two values : 30° and/or 210°.
Now I will  to you to you  that these answers are correct. that these answers are correct.
Indeed, for  = 30° = 30°
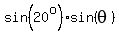 = sin(20°)*sin(30°) = = sin(20°)*sin(30°) = 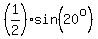 <<<---=== since sin(30°) = <<<---=== since sin(30°) =  . .
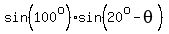 = cos(10°)*sin(-10°) = = cos(10°)*sin(-10°) = 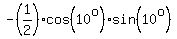 = = 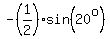 <<<---=== sinse sin(a)*cos(a) = <<<---=== sinse sin(a)*cos(a) = 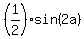 .
Now you see that .
Now you see that  = 30° is the solution: it is PROVED.
Similar proof works for = 30° is the solution: it is PROVED.
Similar proof works for  = 210°. = 210°.
At this point, the wrong solution of @CPhill is disproved completely,
and the right solution is found numerically and proved mathematically.
|
|
|