SOLUTION: If cot²αcot²β = 3, find the value of (2 - cos2α)(2 - cos2β)

Algebra ->  Test  -> Lessons -> SOLUTION: If cot²αcot²β = 3, find the value of (2 - cos2α)(2 - cos2β)       Log On


   

Question 1209582: If cot²αcot²β = 3,
find the value of (2 - cos2α)(2 - cos2β)
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52748) About Me  (Show Source):
You can put this solution on YOUR website!
.
If cot²αcot²β = 3, find the value of (2 - cos2α)*(2 - cos2β).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

There is general formula

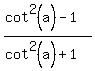    cos(2a) = %28cot%5E2%28a%29-1%29%2F%28cot%5E2%28a%29+%2B+1%29,


valid for any angle "a", where cot(a) is defined.


If you do not know this formula, you can check it immediately on your own.
Its proof uses, essentially, only basic formulas

    sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b)  and  cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).



From this formula, you get

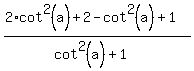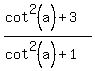    2-cos(a) = 2 - %28cot%5E2%28a%29-1%29%2F%28cot%5E2%28a%29%2B1%29 = %282%2Acot%5E2%28a%29%2B2+-+cot%5E2%28a%29%2B1%29%2F%28cot%5E2%28a%29%2B1%29 = %28cot%5E2%28a%29%2B3%29%2F%28cot%5E2%28a%29+%2B1%29.


Similarly,

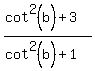    2-cos(b) = %28cot%5E2%28b%29%2B3%29%2F%28cot%5E2%28b%29+%2B1%29.



Therefore,

      (2-cos(2a))*(2-cos(2b)) =  =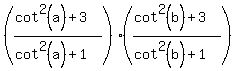 


    =  =


      Now substitute here  cot^2(a)*cot^2(b) = 3,  which is given, 
      into the numerator and the denominator, and continue


    = .


The last ratio is 3.   Therefore, the ANSWER  to the problem's question is 3.

At this point, the problem is solved in full.



Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
I think we can get by just using the standard trig identities that we're
all accustomed to using, even though it might take a little longer:

cot%5E2%28alpha%29cot%5E2%28beta%29%22%22=%22%223

%22%22=%22%223

%22%22=%22%223

%22%22=%22%223

1-sin%5E2%28alpha%29-sin%5E2%28beta%29%2Bsin%5E2%28alpha%29sin%5E2%28beta%29%22%22=%22%223%28sin%5E2%28alpha%29sin%5E2%28beta%29%5E%22%22%29

1-sin%5E2%28alpha%29-sin%5E2%28beta%29%22%22=%22%222%28sin%5E2%28alpha%29sin%5E2%28beta%29%5E%22%22%29

1%22%22=%22%22sin%5E2%28alpha%29%2B+2sin%5E2%28alpha%29sin%5E2%28beta%29%2Bsin%5E2%28beta%29 <-- call this equation 1

Now let's work on

%282-cos%282alpha%29%5E%22%22%29%282-cos%282beta%29%5E%22%22%29



%281%2B2sin%5E2%28alpha%29%5E%22%22%29%281%2B2sin%5E2%28beta%29%5E%22%22%29

1%2B2sin%5E2%28alpha%29%2B2sin%5E2%28beta%29%2B4sin%5E2%28alpha%29sin%5E2%28beta%29



Now look up at equation 1 and you see that what's in the big parentheses
here is equal to 1, so,

1%2B2%281%29%22%22=%22%223

So the answer is 3.

Edwin