Question 1209570: 3^a + 9^a + 27^a = 39
find a
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
3^a + 9^a + 27^a = 39
find a
~~~~~~~~~~~~~~~~~~~~~~
Function a --> 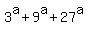 is a monotonically increasing function of "a". is a monotonically increasing function of "a".
At a= 1, we have 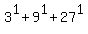 = 3 + 9 + 27 = 39. = 3 + 9 + 27 = 39.
Hence, a= 1 is the unique real solution to the given equation. ANSWER
At this point, the problem is solved completely.
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
3^a + 9^a + 27^a = 39
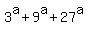 = 39 = 39
 = 39 = 39
 = 39 = 39
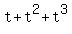 = 39 ------ Substituting t for = 39 ------ Substituting t for 
 <==== The highest exponent is 3, so there're THREE (3) solutions to this equation.
Using the RATIONAL ROOT theorem, we find that 3 is a ROOT of the equation. Therefore, t = 3, so t - 3 = 0, and t - 3
is a factor. With 3 being a root, we use SYNTHETIC DIVISION or LONG DIVISION of POLYNOMIALS to find the other factor.
The former gives us: 3 | 1 | 1 | 1 | - 39 |
| | 3 | 12 | 39 |
| 1 | 4 | 13 | 0 |
Thus, the other factor is: <==== The highest exponent is 3, so there're THREE (3) solutions to this equation.
Using the RATIONAL ROOT theorem, we find that 3 is a ROOT of the equation. Therefore, t = 3, so t - 3 = 0, and t - 3
is a factor. With 3 being a root, we use SYNTHETIC DIVISION or LONG DIVISION of POLYNOMIALS to find the other factor.
The former gives us: 3 | 1 | 1 | 1 | - 39 |
| | 3 | 12 | 39 |
| 1 | 4 | 13 | 0 |
Thus, the other factor is: 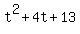 , and so, , and so,  becomes: becomes:  , which gives us:
t - 3 = 0 or , which gives us:
t - 3 = 0 or  t = 3 or The DISCRIMINANT for the quadratic is:
t = 3 or The DISCRIMINANT for the quadratic is:  .
With the DISCRIMINANT being NEGATIVE (< 0), 2 of the roots to this quadratic are
IMAGINARY/COMPLEX.
Since t = 3, the ONLY REAL root is 3.
t = 3 .
With the DISCRIMINANT being NEGATIVE (< 0), 2 of the roots to this quadratic are
IMAGINARY/COMPLEX.
Since t = 3, the ONLY REAL root is 3.
t = 3
 = 3 ------ Back-substituting = 3 ------ Back-substituting  for t for t
 As the BASES are equal, so are the EXPONENTS. As such, a = 1.
As the BASES are equal, so are the EXPONENTS. As such, a = 1.
|
|
|