SOLUTION: If x = (19 + 8√3)^(½) find (x⁴ - 6x³ - 2x² + 18x + 23)/(x² - 8x + 15)

(1)   = .

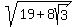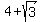         To check and to prove, simply square right side.  You will get then  .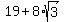



(2)  So, x = .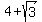  

         It implies  x-4 = ,  (x-4)^2 = 3,  x^2 - 8x + 16 = 3,  x^2 - 8x + 13 = 0.



(3)  Let's calculate the denominator  x^2 - 8x + 15.

         It is  x^2 -8x + 15 = (x^2 - 8x + 13) + 2.

         The part in parentheses is zero, so  the denominator  x^2 - 8x + 15  is simply  2.



(4)  In principle, the numerator can be calculated directly, but it is computationally boring procedure.

     It is simpler to perform a long division.

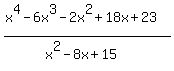            = x^2 + 2x - 1 +  = 

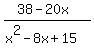         = x^2 + 2x - 1 +  = (x^2 + 2x - 1) + (19 - 10x) = x^2 - 8x + 18 = (x^2 - 8x + 13) + 5.



(5)  The value in the parentheses is zero, as we established above.

     So, we get the 



ANSWER.  If  x = (19 + 8√3)^(1/2),  then    is equal to 5.