Question 1209546: 1) If x + y = 1 and x³ + y³ = 3,
find (1/x³) + (1/y³)
2) If x^(x¹⁶) = 16,
find x²⁰
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a) If x + y = 1 and x³ + y³ = 3,
find (1/x³) + (1/y³)
b) If x^(x¹⁶) = 16,
find x²⁰
~~~~~~~~~~~~~~~~~~~~~~
Part (a)
a) If x + y = 1 and x³ + y³ = 3, find (1/x³) + (1/y³).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Start from
x + y = 1.
Raise it in degree 3. You will get
1 = (x+y)^3 = x^3 + 3x^2*y + 3x*y^2 + y^3 = (x^3 + y^3) + 3xy(x+y).
Replace here x^3 + y^3 by 3 (since it is given), and replace x+y by 1. You will get
1 = 3 + 3xy ,
3xy = -2,
xy =  .
Now .
Now  + + 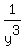 = = 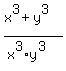 = = 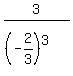 = = 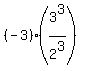 = = 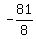 .
ANSWER. At given condition, .
ANSWER. At given condition,  + + 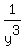 = = 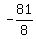 . .
Part (a) is solved.
Part (b)
(b) If x^(x¹⁶) = 16, find x²⁰.
~~~~~~~~~~~~~~~~~~~~~~~~~~
I will give absolutely rigorous mathematical solution, although it will contain element of guessing.
Obviously, the value of x should be greater than 1.
One such value is easy to guess: it is x = 2^(1/4) = 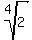 = 1.189207115, approximately.
Indeed, (2^(1/4))^16 = = 1.189207115, approximately.
Indeed, (2^(1/4))^16 = 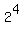 = 16 and, therefore,
x^(x^16) = (2^(1/4))^16 = = 16 and, therefore,
x^(x^16) = (2^(1/4))^16 = 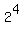 = 16,
so this value of x, x = 2^(1/4) is the solution to the given equation x^(x¹⁶) = 16.
From the other side hand, this function, f(x) = x^(x¹⁶) is a monotonically increasing function
in the domain x > 1, so, there is no other solution to the given equation in this domain.
Thus, for positive real numbers, the only solution
to the given equation x^(x¹⁶) = 16
is x = 2^(1/4) = = 16,
so this value of x, x = 2^(1/4) is the solution to the given equation x^(x¹⁶) = 16.
From the other side hand, this function, f(x) = x^(x¹⁶) is a monotonically increasing function
in the domain x > 1, so, there is no other solution to the given equation in this domain.
Thus, for positive real numbers, the only solution
to the given equation x^(x¹⁶) = 16
is x = 2^(1/4) = 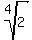 = 1.189207115 (approximately).
CHECK. = 1.189207115 (approximately).
CHECK. 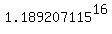 = 16; therefore, x^(x¹⁶) = x^16 = 1.189207115^16 = 16, which is correct.
Now, = 16; therefore, x^(x¹⁶) = x^16 = 1.189207115^16 = 16, which is correct.
Now,  = (2^(1/4))^20 = 2^5 = 32.
ANSWER. Under given condition, = (2^(1/4))^20 = 2^5 = 32.
ANSWER. Under given condition,  = 32. = 32.
Solved completely, with all necessary explanations.
|
|
|