SOLUTION: a + b + c = 6 a² + b² + c² = 14, find the value of a⁸ + b⁸ + c⁸

It is assumed that a, b, c are integer numbers.


From   +  +  = 14  we guess one solution

    a= 3,  b= 2,  c= 1.


Indeed,  then

    3 + 2 + 1 = 6

and

    3^2 + 2^2 + 1^2 = 9 + 4 + 1 = 14.


So, (a,b,c) = (3,2,1) is the basic solution.


There are 5 other solutions that are permutations of the basic triple.


But we should not worry about permutations, since they do not make influence on
the sum   +  + .


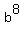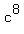Also, it is clear from the equation for squares, that there are no other solutions in integer numbers.


Now we make direct calculation   + 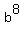 +  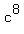=  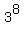+  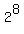+  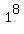= 6818.


ANSWER.  Under given conditions, the sum   + 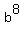 +  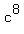 is  6818.