Question 1208295: If 2¹³ + 2¹⁰ + 2ˣ = y²,
find x and y.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll assume x and y are nonnegative integers.
There might be a more clever and elegant solution, but I'm going to check possible values of x.
If x = 0, then,
2^13 + 2^10 + 2^x
= 2^13 + 2^10 + 2^0
= 9217
And,
sqrt(9217) = 96.0052 approximately
Since the square root result isn't a whole number, this shows 9217 isn't a perfect square.
y^2 = 9217 doesn't have an integer solution.
x = 0 won't pair with an integer y value.
We can rule out x = 0.
Let's try x = 1.
2^13 + 2^10 + 2^x
= 2^13 + 2^10 + 2^1
= 9218
And,
sqrt(9218) = 96.0104 approximately
Same idea as the previous paragraph.
We can rule out x = 1.
Let's try x = 2.
2^13 + 2^10 + 2^x
= 2^13 + 2^10 + 2^2
= 9220
And,
sqrt(9220) = 96.0208 approximately
We can rule out x = 2 for similar reasoning as the previous paragraphs.
And so on.
Keep this process going until reaching x = 14.
Use of a spreadsheet is strongly recommended to make this process very quick.
Alternatively you can use a programming language such as Python to write up a quick script.
2^13 + 2^10 + 2^x
= 2^13 + 2^10 + 2^14
= 25600
And,
sqrt(25600) = 160 exactly
We finally get an integer result.
This proves that x = 14 and y = 160 is one ordered pair solution.
2^13 + 2^10 + 2^14 = 160^2
There might be other solutions.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If 2¹³ + 2¹⁰ + 2ˣ = y², find x and y.
~~~~~~~~~~~~~~~~~~~
It is assumed that x and y are integer numbers.
I will give another, strict mathematical solution.
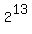 + +  = 9216 = 96^2. (1)
Therefore, = 9216 = 96^2. (1)
Therefore, 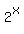 = =  - - 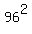 . (2)
Hence, . (2)
Hence, 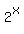 = (y+96)*(y-96). (3)
Thus, = (y+96)*(y-96). (3)
Thus, 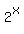 is the product of integers y+96 and y-96.
From it, we conclude that y+96 and y-96 are degrees of 2.
So, we write
y + 96 = is the product of integers y+96 and y-96.
From it, we conclude that y+96 and y-96 are degrees of 2.
So, we write
y + 96 =  y - 96 =
y - 96 = 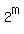 with integer non-negative n and m, and we understand that m < n.
Subtracting the lower equation from the upper one, we get
with integer non-negative n and m, and we understand that m < n.
Subtracting the lower equation from the upper one, we get
 - - 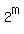 = 192, = 192,
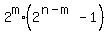 = 192 = 64*3 = = 192 = 64*3 = 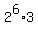 . (4)
From it, we conclude that m = 6, n-m = 2; hence n-6 = 2, n = 8.
Thus y+96 = . (4)
From it, we conclude that m = 6, n-m = 2; hence n-6 = 2, n = 8.
Thus y+96 =  = = 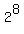 = 256; hence y = 256-96 = 160.
CHECK: y-96 = = 256; hence y = 256-96 = 160.
CHECK: y-96 = 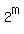 = =  = 64; hence y = 64+96 =160. <<<---=== Check says OK.
Now from (3) = 64; hence y = 64+96 =160. <<<---=== Check says OK.
Now from (3)
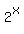 = (y+96)*(y-96) = (160+96)*(160-96) = 16384 = = (y+96)*(y-96) = (160+96)*(160-96) = 16384 = 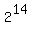 ,
Hence, x = 14.
ANSWER. This problem has two solutions (x,y) = (14,160) and (x,y) = (14,-160).
From where the second, negative value of y came ?
Since right side of equation (1) is y^2, it is clear that with positive solution y= 160,
negative solution y= -160 works, too.
Where we missed it in our reasoning ? - Because in (4), we could take NEGATIVE factors ,
Hence, x = 14.
ANSWER. This problem has two solutions (x,y) = (14,160) and (x,y) = (14,-160).
From where the second, negative value of y came ?
Since right side of equation (1) is y^2, it is clear that with positive solution y= 160,
negative solution y= -160 works, too.
Where we missed it in our reasoning ? - Because in (4), we could take NEGATIVE factors 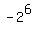 and -3
into consideration. It would lead us to the negative value of y.
But since we just caught this second solution, we shouldn't worry anymore. and -3
into consideration. It would lead us to the negative value of y.
But since we just caught this second solution, we shouldn't worry anymore.
-----------------
Thus the problem is solved completely, using strict mathematical reasoning,
and two solutions in integer numbers are found. All necessary explanations are given.
Happy learning (!)
|
|
|