Question 1208097: If x + 1/x = √3
Find the value of x¹⁸ + x¹² + 1
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The exponents for x^18+x^12+1 are multiples of 6 and multiples of 3.
A clue is to determine the value of x^3.
Let's see what happens when we cube both sides of the original equation.
I'll use the identity (a+b)^3 = a^3+b^3+3ab(a+b) which is a rearrangement of (a+b)^3 = a^3+3a^2b+3ab^2+b^3
x + (1/x) = sqrt(3)
( x + (1/x) )^3 = (sqrt(3))^3
x^3 + (1/x)^3 + 3x*(1/x)*(x+1/x) = (sqrt(3))^2*sqrt(3) ............ use identity for left hand side
x^3 + (1/x)^3 + 3*(x+1/x) = 3*sqrt(3) ............ notice x+(1/x) shows up
x^3 + (1/x)^3 + 3*(sqrt(3)) = 3*sqrt(3) ............ replace it with sqrt(3)
x^3 + 1/(x^3) + 3*sqrt(3) = 3*sqrt(3)
x^3 + 1/(x^3) = 0
x^6 + 1 = 0
x^6 = -1
Then,
x^12 = x^(6*2) = (x^6)^2 = (-1)^2 = 1
x^18 = x^(6*3) = (x^6)^3 = (-1)^3 = -1
x^18 + x^12 + 1 = -1 + 1 + 1 = 1
Therefore,
x^18 + x^12 + 1 = 1 when x + (1/x) = sqrt(3)
--------------------------------------------------------------------------
Another approach is to solve x + (1/x) = sqrt(3) for x.
Then use either solution to compute the value of x^18 + x^12 + 1.
x + (1/x) = sqrt(3)
x^2 + 1 = sqrt(3)*x ............. multiply both sides by x.
x^2 - sqrt(3)*x + 1 = 0
Quadratic formula
x = (-b+-sqrt(b^2-4ac))/(2a)
x = (-(-sqrt(3))+-sqrt((sqrt(3))^2-4*1*1))/(2*1)
x = (sqrt(3)+-sqrt(3-4))/(2)
x = (sqrt(3)+-sqrt(-1))/(2)
x = sqrt(3)/2 + (1/2)i or x = sqrt(3)/2 - (1/2)i
where i = sqrt(-1)
Consider the complex number z = a+bi
It is in cartesian form.
Polar form is z = r*cis(theta) where "cis(theta)" is shorthand for "cos(theta)+i*sin(theta)"
r = sqrt(a^2+b^2) ... due to the Pythagorean Theorem
r = sqrt( (sqrt(3)/2)^2 + (1/2)^2 )
r = sqrt(3/4+1/4)
r = sqrt(1)
r = 1
theta = arctan(b ÷ a)
theta = arctan( (1/2) ÷ (sqrt(3)/2) )
theta = arctan( (1/2) * (2/sqrt(3)) )
theta = arctan( 1/sqrt(3) )
theta = arctan( sqrt(3)/3 )
theta = pi/6 radians
The complex number
x = sqrt(3)/2 + (1/2)i
would be equivalent to the polar form
x = 1*cis(pi/6)
or simply
x = cis(pi/6)
Why are we going through this trouble of converting to polar form?
Because De Moivre's Theorem is very useful.
That theorem states if z = r*cis(theta) then z^n = r^n*cis(n*theta)
So,
x = cis(pi/6)
x^18 = cis(18*pi/6)
x^18 = cis(3pi)
x^18 = cos(3pi) + i*sin(3pi)
x^18 = -1 + i*0
x^18 = -1
And,
x = cis(pi/6)
x^12 = cis(12*pi/6)
x^12 = cis(2pi)
x^12 = cos(2pi) + i*sin(2pi)
x^12 = 1 + i*0
x^12 = 1
So,
x^18 + x^12 + 1 = -1 + 1 + 1 = 1
Therefore,
x^18 + x^12 + 1 = 1 when x + (1/x) = sqrt(3)
A similar question is found here
---------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------
Answer: 1
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If x + 1/x =  , find the value of x^18 + x^12 + 1. , find the value of x^18 + x^12 + 1.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If x + 1/x =  , then , then
 + 1 = + 1 = 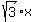
 - - 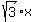 + 1 = 0.
It is the general form of a quadratic equation ax^2 + bx + c = 0
with a= 1, b= + 1 = 0.
It is the general form of a quadratic equation ax^2 + bx + c = 0
with a= 1, b=  , c= 1.
Apply the quadratic formula to find the roots , c= 1.
Apply the quadratic formula to find the roots
 = = 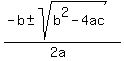 = = 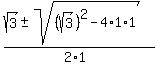 = = 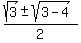 = = 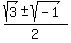 = = 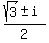 .
So, .
So,  = = 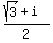 = = 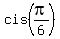 ; ;
 = =  = = 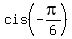 .
Thus .
Thus  is a complex number with the modulus of 1 and the argument of is a complex number with the modulus of 1 and the argument of  . .
 is a complex number with the modulus of 1 and the argument of is a complex number with the modulus of 1 and the argument of 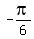 .
For x = .
For x =  = = 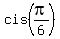 , we have , we have
 + + 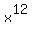 + 1 = + 1 = 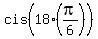 + +  + 1 = + 1 = 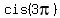 + + 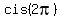 + 1 = -1 + 1 + 1 = 1.
For x = + 1 = -1 + 1 + 1 = 1.
For x =  = = 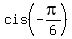 , we have , we have
 + + 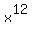 + 1 = + 1 = 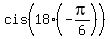 + + 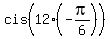 + 1 = + 1 =  + + 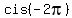 + 1 = -1 + 1 + 1 = 1.
So, for both values of roots, we have + 1 = -1 + 1 + 1 = 1.
So, for both values of roots, we have  + + 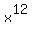 + 1 = 1.
At this point, the solution is complete.
ANSWER. If x + 1/x = + 1 = 1.
At this point, the solution is complete.
ANSWER. If x + 1/x =  , then , then  + + 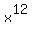 + 1 = 1. + 1 = 1.
Solved.
|
|
|