.
Find x,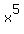 
= 
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
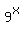
Your starting equation is
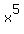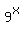= . (1)
Take natural logarithm of both sides
5*ln(x) = x*ln(9).
Divide both sides by ln(x)*ln(9). You will get an EQUIVALENT equation
= 
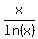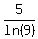. (2)
It is well known fact that the function 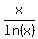has the minimum at x = e,
where e is the base of natural logarithms, e = 2.71828...
The minimum of this function at x= e is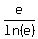 
= 
= e = 2.71828...
From the other side, the value of 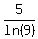is 2.275598067...
THEREFORE, equation (2) has NO solution at x > 0.
ANSWER. In domain x > 0, the given equation (1) has no solution.
Solved.
--------------------
In order to convince yourself visually with the fact that equation (2)
has no solutions, go to website www.desmos.com/calculator.
It allows to plot functions for free automatically.
Print the expression y = 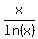, get the plot and compare it with the plot
of horizontal line y = .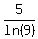
=====================
Post-solution note
This trick with using monotonicity of the function 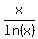is a powerful tool for solving
many/some exponential-polynomial equations, similar to the given in this post
or for proving that such equations have no solutions.
When nothing else does not work, try it . . .
