Question 1206837: Find x,
3ˣ = x⁹
Found 3 solutions by Edwin McCravy, MathLover1, ikleyn:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 If in an equation to solve, the variable to solve for appears both as an
exponent and a non-exponent, as it does here, then there is no way to solve for
the variable other than by iterative methods.
Iterative methods are trial and error processes.
Try a number. If it's too big, try a smaller number.
If it's too small try a bigger number.
Always try a number between the last number you tried that was too big, and
the last number you tried that was too small.
Eventually you will have the solution trapped between two numbers, that get
closer and closer together.
That's a very time-consuming process, but technology can do that trial and
error process instantaneously.
On a TI-84 Plus CE calculator you can get x = 1.1508248, an approximate solution
trapped between 1.15082475 and 1.15082485.
Edwin
If in an equation to solve, the variable to solve for appears both as an
exponent and a non-exponent, as it does here, then there is no way to solve for
the variable other than by iterative methods.
Iterative methods are trial and error processes.
Try a number. If it's too big, try a smaller number.
If it's too small try a bigger number.
Always try a number between the last number you tried that was too big, and
the last number you tried that was too small.
Eventually you will have the solution trapped between two numbers, that get
closer and closer together.
That's a very time-consuming process, but technology can do that trial and
error process instantaneously.
On a TI-84 Plus CE calculator you can get x = 1.1508248, an approximate solution
trapped between 1.15082475 and 1.15082485.
Edwin
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find x, 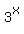 = = 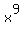 . .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Your starting equation is
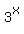 = = 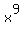 . (1)
Take natural logarithm of both sides
x*ln(3) = 9*ln(x).
Divide both sides by ln(x)*ln(3). You will get . (1)
Take natural logarithm of both sides
x*ln(3) = 9*ln(x).
Divide both sides by ln(x)*ln(3). You will get
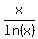 = = 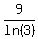 .
Transform right side equivalently multiplying by 1 = .
Transform right side equivalently multiplying by 1 = 
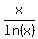 = =  = = 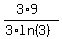 = = 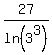 = = 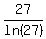 .
Thus we have this equation .
Thus we have this equation
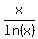 = = 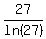 . (2)
It is well known fact that if x > e, then . (2)
It is well known fact that if x > e, then 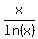 is monotonically increasing function.
Here e is the base of natural logarithms, e = 2.71818...
THEREFORE, from equation (2), we conclude that x = 27 is the unique solution in domain x > e.
ANSWER. In domain x > e, the unique solution to equation (1) is x= 27.
CHECK. At x= 27, left side of equation (1) is is monotonically increasing function.
Here e is the base of natural logarithms, e = 2.71818...
THEREFORE, from equation (2), we conclude that x = 27 is the unique solution in domain x > e.
ANSWER. In domain x > e, the unique solution to equation (1) is x= 27.
CHECK. At x= 27, left side of equation (1) is 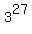 ;
right side of equation (1) is ;
right side of equation (1) is 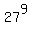 = =  = = 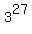 .
Thus, at x= 27, both sides of equation (1) are equal. .
Thus, at x= 27, both sides of equation (1) are equal.
Solved.
-------------------------
Post-solution notes
1. The original equation has the second solution in the domain 1 < x < e, where the function 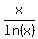 is also monotonic; but this solution is not an integer number.
This second solution can be found numerically as an approximate value.
2. This trick with using monotonicity of the function
is also monotonic; but this solution is not an integer number.
This second solution can be found numerically as an approximate value.
2. This trick with using monotonicity of the function 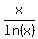 is a powerful tool for solving
many/some exponential-polynomial equations, similar to the given in this post. is a powerful tool for solving
many/some exponential-polynomial equations, similar to the given in this post.
|
|
|