Question 1204820: A nuclear accident is reported in a power plant in an isolated reservation. The location of the power plant and surrounding area is indicated using the following x-y coordinate system, where the power plant is spotted at the origin of the coordinate system.
A straight road runs across the reservation as indicated in the dotted line, that intersects the x and y coordinate axis at 7 km due east (A) and 1.4 km due north (B) from the origin. Scientists are required to set up a camp, adjacent to the road between points A and B, where the radiation level is minimum. Further, the radiation level at a particular location on the first quadrant of the coordinate system was identified as the following function of distances,
Radiation level = 6x+5y²
where x and y are the distance along the x-axis and the y-axis respectively.
a) Formulate the optimization model for the problem.
b) Identify the appropriate optimization technique with justification.
a) Hence obtain a suitable location for a campsite along the road(assume a position on the road), where the radiation level is minimum.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A nuclear accident is reported in a power plant in an isolated reservation. The location of the power plant
and surrounding area is indicated using the following x-y coordinate system, where the power plant is spotted
at the origin of the coordinate system.
A straight road runs across the reservation as indicated in the dotted line, that intersects the x and y
coordinate axis at 7 km due east (A) and 1.4 km due north (B) from the origin. Scientists are required
to set up a camp, adjacent to the road between points A and B, where the radiation level is minimum.
Further, the radiation level at a particular location on the first quadrant of the coordinate system
was identified as the following function of distances,
Radiation level = 6x+5y²
where x and y are the distance along the x-axis and the y-axis respectively.
a) Formulate the optimization model for the problem.
b) Identify the appropriate optimization technique with justification.
 c) Hence obtain a suitable location for a campsite along the road(assume a position on the road), where the radiation level is minimum. c) Hence obtain a suitable location for a campsite along the road(assume a position on the road), where the radiation level is minimum.
~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, the required steps and technique are as described below.
(1) Write an equation of the straight line defined by given points.
(2) From this equation, express x as a function of y.
(3) substitute this expression into the function describing the radiation level.
It will give a radiation function on the road as a function of one variable y.
(4) The last step is to find the minimum of radiation along the road using standard method of Calculus
(or more simple Algebra method, if we are lucky).
Below is an implementation of this general plan.
(1) The road passes throw points A= (7,0) and B= (0,1.4). Hence, the slope is m = 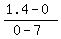 = = 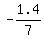 = =  = -0.2.
Thus an equation of the line is y = -0.2(x-7), or y = = -0.2.
Thus an equation of the line is y = -0.2(x-7), or y = 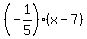 . (1)
Step (1) is complete.
(2) From equation (1) 5y = -x+7, x = 7-5y. (2)
Step (2) is complete.
(3) Substituting x from expression (2) into the radiation function, we get the radiation function on the road in the form
R(y) = . (1)
Step (1) is complete.
(2) From equation (1) 5y = -x+7, x = 7-5y. (2)
Step (2) is complete.
(3) Substituting x from expression (2) into the radiation function, we get the radiation function on the road in the form
R(y) =  = = 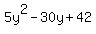 . (3)
Step (3) is complete. We have now the radiation function on the road as a quadratic function of one coordinate y.
(4) In some sense, we are really lucky. Since function R(y) is quadratic (= parabola), we can find its minimum value
using Algebra only, without using Calculus. Extremum of R(y) (actually, the minimum) is achieved at the point . (3)
Step (3) is complete. We have now the radiation function on the road as a quadratic function of one coordinate y.
(4) In some sense, we are really lucky. Since function R(y) is quadratic (= parabola), we can find its minimum value
using Algebra only, without using Calculus. Extremum of R(y) (actually, the minimum) is achieved at the point
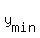 = " = "  " = " = 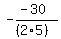 = =  = 3,
and the level of radiation there is R(3) = = 3,
and the level of radiation there is R(3) =  = -3.
+-------------------------------------------------------------------------------+
| By the way, the fact that the radiation level is negative, tells us |
| that this function R(y) is not applicable there - see my discussion below. |
+-------------------------------------------------------------------------------+
But notice that this point with y-coordinate = -3.
+-------------------------------------------------------------------------------+
| By the way, the fact that the radiation level is negative, tells us |
| that this function R(y) is not applicable there - see my discussion below. |
+-------------------------------------------------------------------------------+
But notice that this point with y-coordinate 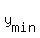 = 3 is out of the working interval [0,1.4] for "y"
in the first quadrant. Actually, the point with coordinate = 3 is out of the working interval [0,1.4] for "y"
in the first quadrant. Actually, the point with coordinate 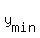 = 3 lies in the second quadrant.
Regarding quadrant 2, we have no expression for the radiation function there; according to the problem, it is not defined
there - so, we can not move in the second quadrant and can not develop our reasonings there.
It means that we should look at values of the function R(y) at the endpoints of the road in first quadrant,
which are y= 0 and y= 1.4.
At y= 0 we have R(0) = according to (3) = = 3 lies in the second quadrant.
Regarding quadrant 2, we have no expression for the radiation function there; according to the problem, it is not defined
there - so, we can not move in the second quadrant and can not develop our reasonings there.
It means that we should look at values of the function R(y) at the endpoints of the road in first quadrant,
which are y= 0 and y= 1.4.
At y= 0 we have R(0) = according to (3) = 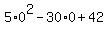 = 42.
At y= 1.4 we have R(1.4) = according to (3) = = 42.
At y= 1.4 we have R(1.4) = according to (3) = 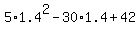 = 9.8.
From it, we conclude that along the road in the first quadrant, the radiation level has the minimum
at the point y= 1.4, which corresponds to point B.
So, the camp should be located at point B, according to the given restrictions/requirements.
ANSWER. The camp should be located at point B. = 9.8.
From it, we conclude that along the road in the first quadrant, the radiation level has the minimum
at the point y= 1.4, which corresponds to point B.
So, the camp should be located at point B, according to the given restrictions/requirements.
ANSWER. The camp should be located at point B.
Solved.
/////////////////////
What is strange in this problem from the common sense of view is that the radiation level function
has this form 6x + 5y^2.
From the common sense of view, this function should depend on the radius only,
(on the distance from the origin) and should monotonically decrease from the origin,
if an accident happened at the origin.
So, any physicist (and any person having common sense) will be confused / (perplexed)
by such formulation. But, from the other side, it is a Math problem, so perhaps we should not
ask such questions, at all.
Nevertheless, keep it in mind (and tell it to your professor/boss) that from the side, it looks ABSURDIST.
Do not distribute (do not spread) it in the Internet so as not to embarrass yourself.
Having such "radiation level function", the best location to place a camp is the epicenter at the origin,
because the radiation level is ZERO there, meaning that there is no radiation at the camp.
Surely, it is very ludicrous answer - but it is correct, in the context of given radiation function.
Every day at this forum, I see incoming "problems" that contradict
to common sense or are incorrect, so it just does not surprise me.
My duty is only to warn the customers about deficiencies that I see in their problems.
|
|
|