Question 1204175: P can complete a task in x days while Q takes (x + 12) days to do the same task.
a) What fraction of the task can each of them complete in a day?
b) If both of them work together, they can
complete the task in 8 days. Find x.
Found 2 solutions by Edwin McCravy, Theo:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website! P can complete a task in x days while Q takes (x + 12) days to do the same task.
a) What fraction of the task can each of them complete in a day?
P can complete 1 task in x days, so P can complete 1/x of a task in 1 day.
Q can complete 1 task in (x + 12) days, so Q can complete 1/(x + 12) of a task
in 1 day.
b) If both of them work together, they can
complete the task in 8 days. Find x.
P can complete 1/x of a task in 1 day, so P can complete 8/x of a task in 8
days.
Q can complete 1/(x + 12) of a task in 1 day, so Q can complete 8/(x + 12) of a
task in 8 days.
So together, they can complete 8/x + 8/(x+12) of a task in 8 days
That's 1 task, so
  
LCD = x(x + 12)
 
 
 
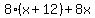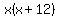
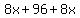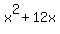
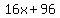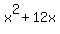
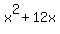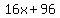
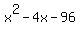
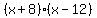x+8=0; x-12=0
x=-8; x=12
x cannot be negative.
x = 12.
Now that we have x, we can answer (a) as a numerical fraction:
a) What fraction of the task can each of them complete in a day?
P can complete 1 task in 12 days, so P can complete 1/12 of a task in 1 day.
Q can complete 1 task in (12 + 12) = 24 days, so Q can complete 1/(12 + 12) = 1/24 of a task in 1 day. Edwin
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! let p = the rate that P works per day.
let q = the rate that Q works per day.
rate * time = quantity.
for P, you get p * x = 1, resulting in p = 1/x
for Q, you get q * (x + 12) = 1, resulting in q = 1/(x + 12).
you are given that they can both complete the task in 8 days when working together.
the equation for that is 8 * (p + q) = 1
simplify to get 8p + 8q = 1
since p = 1/x and q = 1/(x + 12), you get:
8 * 1/x + 8 * 1/(x + 12) = 1
simplify to get 8/x + 8/(x + 12) = 1
multiply both sides of this equation by x * (x + 12) to get:
8 * (x + 12) + 8 * x = x * (x + 12)
simplify to get:
8x + 96 + 8x = x^2 + 12x
combine like terms to get:
16x + 96 = x^2 + 12x
subtract the left side of the equation from both sides of the equation to get:
0 = x^2 + 12x - 16x - 96
combine like terms to get:
0 = x^2 - 4x - 96
solve this quadratic equation to get:
x = 12 or x = -8.
since x has to be positive, then x = 12.
since p = 1/x, then p = 1/12
since q = 1/(x + 12), then q = 1/24
since 8p + 8q = 1, then replace p and q with their respective values to get:
8 * 1/12 + 8 * 1/24 = 1
simplify to get 8/12 + 8/24 = 1
simplify further to get 1 = 1, confirming the value of p and q are good.
answers to your questions are:
a) What fraction of the task can each of them complete in a day?
P can complete 1/12 of the task in one day.
Q can complete 1/24 of the taxk in one day.
b) If both of them work together, they can complete the task in 8 days. Find x.
x is equal to 12.
|
|
|
