SOLUTION: Topic : Discrete Random Variable (Geometric Distribution) Repeated independent trials are carried out in which the probability of success in each trial is 0.66 . Correct to 3 sig

Let Y means successful trial;  N means unsuccessful trial.


(a)  In case (a), they want you find the probability of this event:  NNY.

     So, 1st trial is N (with the probability 1-0.66 = 0.34);
         2nd trial is N (with the probability 1-0.66 = 0.34);
         3rd trial is Y (with the probability 0.66.


     The probability of the event NNY is  P(NNY) = 0.34*0.34*0.66 = 0.076296  (precise value).    ANSWER to question (a)



(b)  The favorable events are    Y    NY  
     (two favorable events, and they, obviously, are disjoint).


     So, the probability under the problem's question is

         P = P(Y) + P(NY) = 0.66 + 0.34*0.66 = 0.8844  (precise value).    ANSWER to question (b)



(c)  After solutions (a) and (b), you are just prepared ENOUGH to understand that

         P = P(N) + P(NN) + P(NNN) + P(NNNY) + P(NNNNY) + P(NNNNNY) + . . . (infinite series).


     Next, first three terms of this infinite sum are

         P(N) = 0.34;

         P(NN) = 0.34*0.34 = 0.1156;

         P(NNN) = 0.34^3   = 0.039304.


     The following terms  P(NNNY) + P(NNNNY) + P(NNNNNY) + . . . (infinite series) 
     represent the sum of an INFINITE geometric progression with the first term a = 0.34^3*0.66
     and the common ratio of r = 0.34.

     So, the sum of these following terms is 

         P(NNNY) + P(NNNNY) + P(NNNNNY) + . . . (infinite series) =  =  =  =  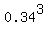= 0.039304  (rounded).


     Finally, the answer to question (c) is this sum

         P = 0.34 + 0.1156 + 0.039304 + 0.039304 = 0.534208  (precise value),  

             or  0.534,  rounded as requested.    ANSWER to question (c)