SOLUTION: The letters of the word MATHEMATICS are written, one on each of 11 separate cards. The cards are laid out in a line. a. Calculate the number of different arrangements of these let

Algebra ->  Test  -> Lessons -> SOLUTION: The letters of the word MATHEMATICS are written, one on each of 11 separate cards. The cards are laid out in a line. a. Calculate the number of different arrangements of these let      Log On


   

Question 1203283: The letters of the word MATHEMATICS are written, one on each of 11 separate cards. The cards are laid out in a line.
a. Calculate the number of different arrangements of these letters.
b. Determine the probability that the vowels are placed together.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
The letters of the word MATHEMATICS are written, one on each of 11 separate cards.
The cards are laid out in a line.
(a) Calculate the number of different arrangements of these letters.
(b) Determine the probability that the vowels are placed together.
~~~~~~~~~~~~~~~~~~~~~ 

(a)  The word MATHEMATICS has 11 letter.

     Of them, letters M, A, T are repeating; the other 8 = 11-3 letters are unique.

     Letter M has multiplicity 2; the same with letters A and T.


     Therefore, the number of different arrangements of the letters of word MATHEMATICS is

         11%21%2F%282%21%2A2%21%2A2%21%29 = %281%2A2%2A3%2A4%2A5%2A6%2A7%2A8%2A9%2A10%2A11%29%2F%282%2A2%2A2%29 = 4,989,600.    ANSWER



(b)  The block of vowels is AEAI.  It consists of 4 letters.

     The other 11-4 = 7 letters are consonants.

     When we consider arrangements, the block of vowels can be placed in any of 7+1 = 8 
     possible positions between consonants, or before consonants, or after consonants.
     It gives 8 possible options.

     Next, there are 4! = 24 possible permutations inside this block,
     and there are 7! possible permutations of consonants outside of this block.


     So, the total number of such permutations for word MATHEMATICS is the product
             8*4!*7!

     To get the number of possible arrangements, we still (or again) must divide it by the factor (2!*2!*2!).


     So, the number of all possible arrangements of this type (b) is  

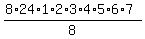          %288%2A4%21%2A7%21%29%2F%282%21%2A2%21%2A2%21%29 = %288%2A24%2A1%2A2%2A3%2A4%2A5%2A6%2A7%29%2F8 = 120,960.    


     The desired probability is the ratio of numbers  120,960  and  4,989,600

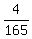         P = 120960%2F4989600 = 4%2F165 = 0.02424  (rounded).    ANSWER

Solved.



Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
The letters of the word MATHEMATICS are written, one on each of 11 separate
cards. The cards are laid out in a line.
a. Calculate the number of different arrangements of these letters.
If all 11 letters of MATHEMATICS were distinguishable, the answer would be 11!.
But since the two M's are indistinguishable we must divide by 2!. Same for the A's and T's.

So that's 11%21%2F%282%212%212%21%29%22%22=%22%224989600%29

b. Determine the probability that the vowels are placed together.

We begin by finding the permutations of consonants MTHMTCS.
There are 7%21%2F%282%212%21%29%22%22=%22%221260

Then for every arrangement of consonants, for instance for MTHMTCS, we place 8
blanks.

____M____T____H____M____T____C____S____

and pick one of the 8 blanks to put all 4 vowels together in.  We can do that in
8 ways.

The 4 vowels AEAI can be arranged in 4%21%2F2%21%22%22=%22%2212 ways.

So the number of successful ways is (1260)(8)(12) = 120960 ways.

So the desired probability is 120960%2F4989600%22%22=%22%224%2F165

Edwin