Question 1166417: In a certain region, the electric potential due to a charge distribution is given by the equation V(x,y,z) = 3x^2y^2+ yz^3-2z^3x, where x, y,andzare measured in meters and Vis in volts. Calculate the magnitude of the electric field vector at the position (x,y,z) = (1.0, 1.0, 1.0).
Answer by ikleyn(52775)   (Show Source):
You can put this solution on YOUR website! .
Electric field E has the components
 =  ,
 =  ,
 =  .
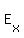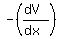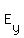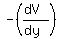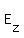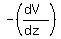So, take the partial derivatives of the potential V(x,y,z) in each direction x, y, z,
and you will get the electric field vector.
Then substitute the values x= 1, y= 1 and z= 1 into these expressions, and calculate.
The vector which you get at the end, will be your answer.
-----------
To read guiding materials, see this link
https://medium.com/@rjallain/using-the-electric-potential-to-find-the-vector-electric-field-d551df37d296
Have fun (!)
|
|
|
