Question 1166005: 2tan^2x=3secx-3
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is 2 * tan^2(x) = 3 * sec(x) - 3.
tan^2(x) = sin^2(x) / cos^2(x).
since sin^2(x) + cos^2(x) = 1, you get:
sin^2(x) = 1 - cos^2(x).
therefore:
sin^2(x) / cos^2(x) = (1 - cos^2(x)) / cos^2(x).
this is equal to 1 / cos^2(x) - cos^2(x) / cos^2(x).
this is equal to 1 / cos^2(x) - 1.
this is equal to sec^2(x) - 1.
we have established that tan^2(x) is equal to sec^2(x) - 1
as a test to see if this is true, pick any angle between 0 and 90 degrees, but not 0 nor 90 degrees.
i picked 75 degrees.
my calculator is set to degrees.
tan^2(75) = tan(75)^2 = 13.92820323
sec^2(75) - 1 = sec(75)^2 - 1 = 1 / cos(75)^2 - 1 = 13.92820323.
they are equivalent.
therefore i can use sec^2(x) - 1 in place of tan^2(x).
back to the problem.
the problem states that 2 * tan^2(x) = 3 * sec(x) - 3
since tan^2(x) = sec^2(x) - 1, then 2 * tan^2(x) = 3 * sec(x) - 3 becomes:
2 * (sec^2(x) - 1) = 3 * sec(x) - 3
simplify this to get:
2 * sec^2(x) - 2 = 3 * sec(x) - 3
subtract sec(x) from both sides of the equation and add 3 to both sides of the equation to get:
2 * sec^2(x) - 2 - sec(x) + 3 = 0
combine like terms and order the terms in descending order of degree to get:
2 * sec^2(x) - sec(x) + 1 = 0
this is a quadratic equation that can be factored to get:
(2 * sec(x) - 1) * (sec(x) - 1) = 0
solve for sec(x) to get:
sec(x) = 1/2 or sec(x) = 1
since sec(x) = 1 / cos(x), then these equations become:
1 / cos(x) = 1/2 or 1 / cos(x) = 1
solve for cos(x) to get:
cos(x) = 2 or cos(x) = 1
cos(x) can't be greater than 1, so the only possible answer is sec(x) = 1
when sec(x) = 1, the angle is 0 degrees plus or minus k * 360 degrees, where k is a non-negative integer.
your solution is that x = 0 degrees plus or minus k * 360 degrees.
if you restrict the answer to between 0 and 360 degrees, than x will be either 0 or 360 degrees.
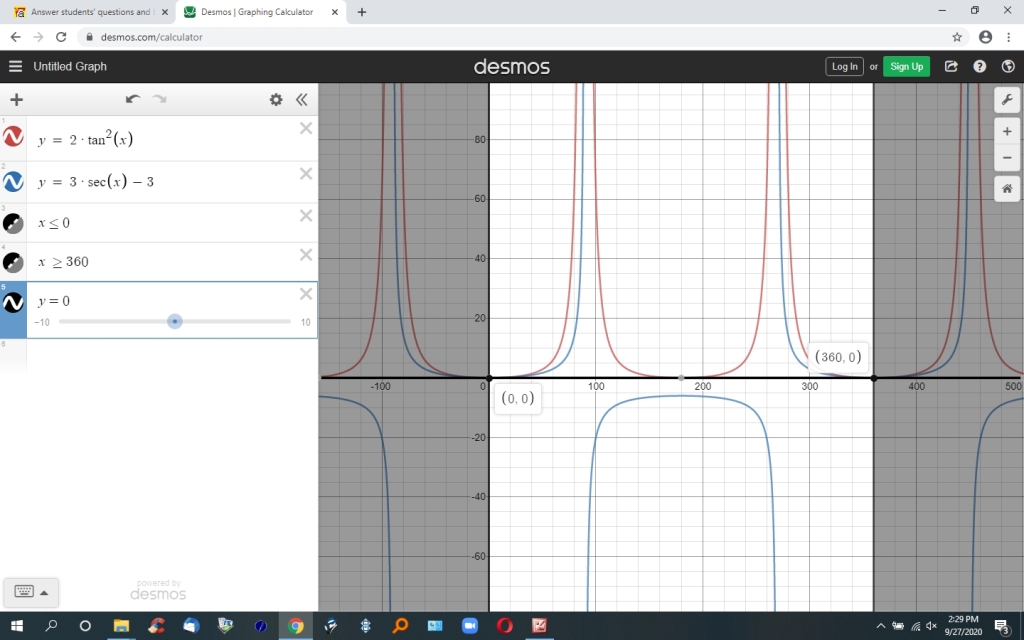
the equation can be graphed as follows:
y = 2 * tan^2(x) is one equation.
y = sec(x) - 3 is another equation.
the intersection of these two equations will be your solution.
here's the graph showing the solution restricted to from 0 to 360 degrees.
here's the graph showing the solution going out to multiples of 360 degrees in both directions (not too many because then it becomes difficult to see).
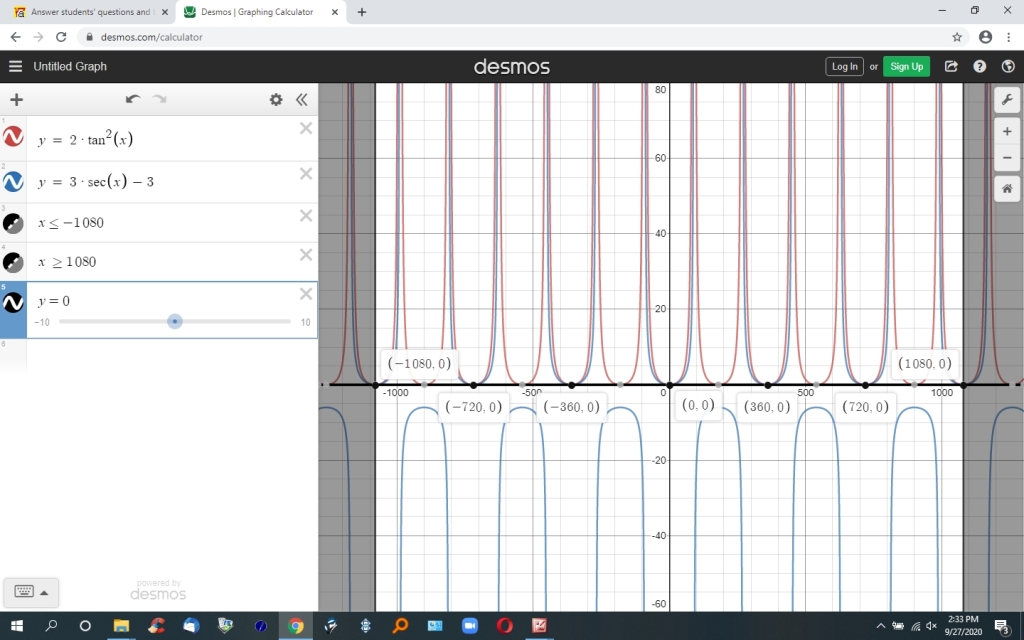
i took the multiple 360 degree solution to plus or minus 1080 degrees.
that's enough to show you that the solution repeats endlessly in each direction.
your solution in the multiple 360 degree graph is
x = 0, 360, 720, 1080 and x = -360, -720, =1080 degrees.
in other words, the solution repeats every 360 degrees in either direction from 0.
Answer by greenestamps(13198)   (Show Source): (Show Source):
|
|
|