SOLUTION: It took Jim 25 minutes to ride to the bicycle shop and 1 hour and 15 min to walk home. If he can ride his bike 8 km/hr faster than he can walk, how far is the repair shop? Thank

Algebra ->  Test  -> Lessons -> SOLUTION: It took Jim 25 minutes to ride to the bicycle shop and 1 hour and 15 min to walk home. If he can ride his bike 8 km/hr faster than he can walk, how far is the repair shop? Thank       Log On


   

Question 1165976: It took Jim 25 minutes to ride to the bicycle shop and 1 hour and 15 min to walk home. If he can ride his bike 8 km/hr faster than he can walk, how far is the repair shop?
Thank you!
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
15 minutes is 1%2F4 hour.
25 minutes is 5%2F12 hour. 
             SPEED          TIME          DISTANCE
RIDE TO        r+8          5%2F12        d
WALK Back      r           1%261%2F4        d

This is not the only way, but the distances d being equal each way,
%28r%2B8%29%2A%285%2F12%29=%28r%29%281%261%2F4%29
Solve this for r, and then evaluate %285%2F4%29r.

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
It took Jim 25 minutes to ride to the bicycle shop and 1 hour and 15 min to walk home.
If he can ride his bike 8 km/hr faster than he can walk, how far is the repair shop?
~~~~~~~~~~~~~~ 


Another way to solve the problem is to notice that 1 hour and 15 minutes is  75 minutes

and the ratio of traveled times is 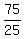 75%2F25 = 3.


It means that the rate cycling is 3 times the rate walking,

So, the rate cycling is 3x, where x is the rate walking.


But the difference of the rates is

    3x - x = 8 km/h,   or

    2x     = 8 km/h,

     x     = 8/2 = 4 km/h.


So, to find the distance, multiply the rate walking, or 4 km/h, by the time walking, which is 1 hour and 15 minutes, ot 5%2F4  hours.
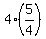You will get then the distance = 4%2A%285%2F4%29 = 5 kilometers.    ANSWER

Solved.