SOLUTION: . Determine the value(s) of k such that the angle between the vector a = (1, 1, k) and b = (1, 0, 1) is 45°. There are little arrows above vectors a and b.. Tha

Use the formula  

     = ,    (1)


where (a*b) is the scalar product of the vectors and  |a|  and  |b|  are the lengths of these vectors.  

  is the angle between the given vectors.


In your case

    (a*b) = 1*1 + 1*0 + k*1 = k+1;

    |a| =  = ;

    |b| =  = .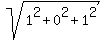


So, your equation (1) becomes


     = .


Simplify it step by step

    
     = 

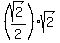    1  = 

     = k+1

    k^2 + 2 = (k+1)^2

    k^2 + 2 = k^2 + 2k + 1

    2 = 2k + 1

    2 - 1 = 2k

    1     = 2k

    k =  = 0.5.    ANSWER