SOLUTION: Consider the cubic function {{{ f(x) = ax^3 + bx^2 + cx + d }}}. Determine the values of a, b, c, and d so that all of the following conditions are met. a. f '(-1) = 1, f '(0)

The condition (c) gives us  d = f(0) = -3.

So, the value of d is joust found.



The condition (a)  f'(-1) = 1 leads to this equation

    f'(-1) = 3a*(-1)^2 + 2b(-1) + c = 1,  or

             3a        - 2b     + c = 1.    (1)



The condition (a)  f'(0) = -2 leads to this equation

    f'(0)  = 3a*0^2 + 2b*0 + c = -2,  or

                             c = -2.        (2)   

So, the value of c is just found:  c = -2.



The condition (b) means that the second derivative of f(x) has zero value at the point x= 1

    f''(1) = 0,  or

    6a + 2b = 0.                              (3)



        By the way, the condition (b)  also means that the point (1,0) lies on the curve y = f(x),  or  f(1) = 0.

        It is a "hidden", an ADDITIONAL and an EXCESSIVE condition, which makes the solution impossible and non-existing, as you will see it later.



So, we just have two equation to determine two remaining unknown coefficients "a" and "b"

    3a - 2b = 3                               (4)   (obtained from (1) and (2))

    6a + 2b = 0                               (5)   (it is equation (3))


To solve this system, add equations (4) and (5).  You will get then

    9a      = 3,


which implies  a = .


Then from (4),  2b = - 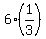 = -2;  hence,  b = -1.


So, we just found all coefficients  a = ;  b = -1;  c = -2  and  d = -3.  

         y = f(x) = .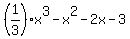


CHECK

    (a)  f'(-1) = 3*(1/3)*(-1)^2 - 2*(-1) - 2 = 1 + 2 - 2 = 1.   ! Correct !

    (a)  f'(0)  = -2.                                            ! Correct !

    (b)  f''(1) = 3*2*(1/3) - 2*1 = 2 - 2 = 0                    ! Correct !

         Now I should check the "hidden" condition that the point (1,0) lies on the curve.

         f(1) = 3*(1/3) - 2*1 - 2*1 - 3 = 1 - 2 - 2 - 3 = -6 =/= 0    ! Incorrect !


The conclusion.  As worded and presented, the given problem is self-contradictory and has no solution.

    Had the problem said  "there is a point of inflection at  x = 1", the problem would have a solution as shown above.


    But in the form  "there is a point of inflection at (1,0)", it brings a "hidden" condition that the point (1,0) lies
    
    on the curve.  With this hidden condition, we have 4+1 = 5 equations for four unknowns.

    These 5 equations are INCONSISTENT, which makes the solution in this form IMPOSSIBLE and NON-EXISTING.