Question 1128664: Use the function f and the given real number a to find (f^ −1)'(a).
f(x) = x3 + 5x − 1, a = −7
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem asks you to find the value of x for which the value of the given function is -7. So


Synthetic substitution (or any of a number of other methods) finds a real solution is x = -1; it turns out the other two solutions are complex. So
ANSWER: f^(-1)(-7) = -1
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Use the function f and the given real number a to find (f^ −1)'(a).
f(x) = x3 + 5x − 1, a = −7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem asks you to find the value of the DERIVATIVE of the inverse function g(y) to the given function
y = f(x) = x^3 + 5x -1
at the point y= f(x) = -7.
The key idea in solving the problem is to use WELL KNOWN identity
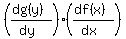 = 1. (1)
Our first step is to determine the value of "x".
For it, we first solve the equation
x^3 + 5x - 1 = -7, (2)
which is equivalent to
x^3 + 5x + 6 = 0. (3)
It easy to guess and then to check that x= -1 is the solution.
Then performing long division or synthetic division of the given polynomial by (x+1), you find the second polynomial factor,
which has complex roots; so, the equation (2) has UNIQUE real solution x= -1.
I do not go into details here, since it is only an auxiliary melody - not the main theme.
Thus we know that x= -1 is the solution to (2), and we easily can calculate the derivative = 1. (1)
Our first step is to determine the value of "x".
For it, we first solve the equation
x^3 + 5x - 1 = -7, (2)
which is equivalent to
x^3 + 5x + 6 = 0. (3)
It easy to guess and then to check that x= -1 is the solution.
Then performing long division or synthetic division of the given polynomial by (x+1), you find the second polynomial factor,
which has complex roots; so, the equation (2) has UNIQUE real solution x= -1.
I do not go into details here, since it is only an auxiliary melody - not the main theme.
Thus we know that x= -1 is the solution to (2), and we easily can calculate the derivative 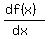 at this point: it is at this point: it is
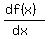 = = 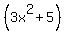 at x= -1, which is 3*(-1)^2+5 = 3+5 = 8.
Then, according to (1), for the inverse function g(y) to function f(x), we have at x= -1, which is 3*(-1)^2+5 = 3+5 = 8.
Then, according to (1), for the inverse function g(y) to function f(x), we have
 = = 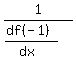 = =  . ANSWER
It is what the problem asks to get.
ANSWER. (f^(-1))'(-7) = . ANSWER
It is what the problem asks to get.
ANSWER. (f^(-1))'(-7) =  . .
Solved.
-----------------
Tutor @greenestamps misread the problem, so his answer and his solution are IRRELEVANT.
|
|
|