Question 1118715: A mass is hung from a spring and set in motion so that it oscillates continually up and down. The velocity v of the weight at time t is given by the equation
v=−3cos(3πt)
with v measured in feet per second and t measured in seconds. Determine the maximum velocity of the mass and the amount of time it takes for the mass to move from its lowest position to its highest position.
What is the maximum velocity?
The time from high to low?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you graph this equation, you will find that it looks like this:
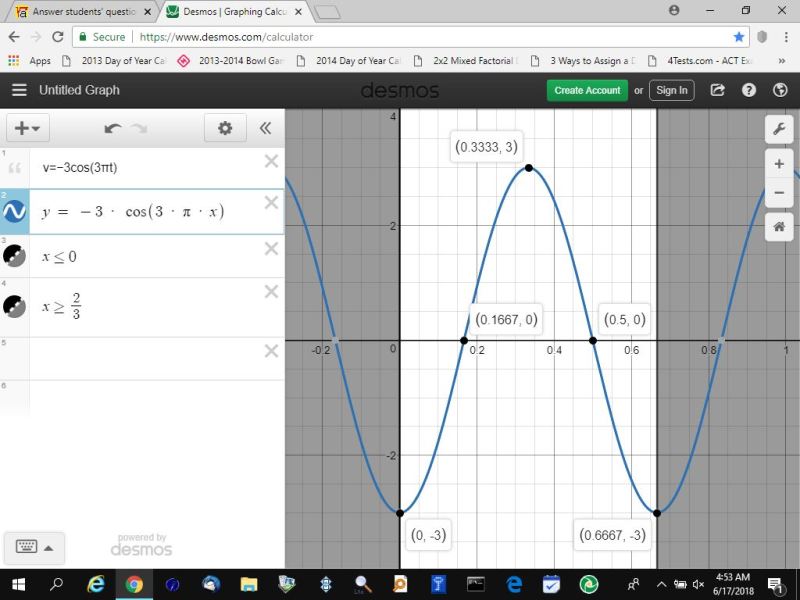
this is a cosine function with an amplitude of -3 and a frequency of 2/3 and a center line at y = 0.
to graph this equation, i made y represent v and x represent t.
therefore y = velocity in feet per second and x = time in seconds on the graph.
the cosine function normally has a period of 2 * pi and an amplitude of 1.
the general equation for the cosine function is:
y = a * (b * (x - c)) + d
a is the amplitude which is the distance from each peak to the center line which is halfway between the high peak and the low peak.
b is the frequency which is the number of cycles in 2 * pi radians.
the function repeats every cycle.
one full cycle is called the period of the cosine function.
c is the horizontal displacement which is the distance left or right from where the value of x would have been without the displacement.
d is the vertical displacement which is the distance up or down from where the center line value of y would have been without the displacement.
the distance from the high peak to the center line is the same as the distance from the low peak to the center line unless some external force is acting on it to make it behave differently over time.
the default value of a and b is 1 and the default value of c and d is 0.
this means the default value of the amplitude and the frequency is 1 and the default value of the horizontal displacement and vertical displacement is 0.
your default cosine equation is therefore y = cos(x).
this is the same as y = a * (b * (x-c)) + d where a = 1 and b = 1 and c = 0 and d = 0.
the default cosine function would normally start at y = 1 and go to y = -1 and then back up to y = 1.
that would be one complete cycle.
if the amplitude is 3, then it would start at y = 3 and go to y = -3 and then back up to y = 3.
when you make the amplitude negative, then it reverses and it starts at y = -3 and goes to y = 3 and then back down to y = -3 in one full cycle.
the freuency is normally set at the default of 1.
the period, which is the number of radians in one full cycle, is normally 2 * pi.
the formula for period is 2 * pi / frequency.
the formula for frequency is (2 * pi) / period.
when the frequency is 1, period = (2 * pi) / 1 = 2 * pi.
when the period is 2 * pi, the frequency is (2 * pi) / (2 * pi) = 1.
in your equation, the frequency is equal to 3 * pi.
the period is therefore equal to 2 * pi / (3 * pi) = 2/3.
that's the number of radians it takes to complete one full cycle of the cosine function.
the frequency was set up in such a way so that the period in radians is the same as the time in seconds.
therefore, the cosine function will complete one full cycle in 2/3 radians which will take 2/3 seconds.
y represents the velocity of the mass connected to the coil in feet per second.
x represents the number of seconds.
depending on how you look at it, negative velocity could be the mass moving in a downward direction and positive velocity could be the mass moving in an upward direction, or vice versa.
i'll assume the mass is moving in a downward direction when the velocity is negative.
it's time to look at the graph again.

at x = 0 seconds, the mass is moving in a downward direction at the rate of 3 feet per second.
this is shown on the graph as the point (0,-3).
1/6 of a second later, the velocity is 0 which means the mass is not moving either down or up.
this is shown on the graph as the point (.1667,0).
this occurs when the mass has traveled to it's farthest in a downward direction and will start going back up again because the spring was stretched to its maximum and will now be pulling the mass back up.
in another 1/6 of a second, the elapsed time will be 1/3 of a second and the mass will be moving upwards at its maximum velocity of 3 feet per second.
this is shown on the graph as the point (.3333,3).
in another 1/6 of a second, the elapsed time will be 3/6 = 1/2 seconds and the mass will have reached its maximum position in an upward direction and will start being pulled back down again by some force, which could be the force of gravity unless some other force is pulling it back down.
this is shown on the graph as the point (.5,0).
in anaother 1/6 of a second, the elapsed time will be 2/3 seconds and the mass is now being pulled back down at a maximum valocity of 3 feet per second.
this is shown on the graph as the point (2/3,-3).
this completes one full cycle which repeats every 2/3 seconds endlessly.
note that the equation is not telling you how far the mass is moving.
it is only telling you how fast the mass is moving and in what direction.
you can figure out how far the mass is moving in either direction if you know the equations for translating the feet per second from the graph into feet.
i'll get into that a little later, but for now, the point is that the equation doesn't tell you how far the mass is moving in either direction, only how fast.
back to your questions.
they are:
Determine the maximum velocity of the mass and the amount of time it takes for the mass to move from its lowest position to its highest position.
What is the maximum velocity?
The time from high to low?
the maximum velocity of the mass will be 3 feet per second in either a positive direction or in a negative direction.
this maximum velocity is shown in the graph at the points (0,-3), (.3333,3),(.6667,-3).
that's at 0 seconds, 1/3 seconds, 2/3 seconds.
that tells you that it takes 1/3 seconds for the mass to go from maximum velocity in a positive direction to maximum velocity in a negative direction and vice versa.
the answer to the questions is therefore:
start of answer ...................
the maximum velocity is 3 feet per second in either direction.
if you presume the highest velocity is 3 feet per second in a positive direction and the lowest velocity is 3 feet per second in a negative direction, then it takes 1/3 seconds to go from the highest velocity to the lowest velocity.
if you presume that the highest velocity in either direction is 3 feet per second and the lowest velocity is 0 feet per second, then it takes 1/6 seconds to go from the highest velocity to the lowest velocity.
end of answer ...................
once again, the y value on the graph is showing you the velocity, or the feet per second that it is moving at and in what direction.
the y value is not showing you how far the mass is traveling in either direction.
i did a little brute force analysis to determine how far the mass was moving in each direction.
the results show that the approximate distance the mass is moving would be about .6363 feet in either direction.
this is a brute force approximation using excel and dividing the intervals 1/120 seconds each.
a more exact number would involve calculus integration.
i used an online integration calculator and it came up with total movement between 1/6 seconds and 1/2 seconds of approximately 0.6366 feet.
the graph shows that the velocity is 0 at 1/6 seconds and goes to a maximum positive velocity of 3 and then back to 0 at 1/2 seconds.
that interval represents the total movement of the mass in a positive direction.
there is an equal movement of the mass in a negative direction.
it appears that the brute force calculation wasn't all that bad.
all of this is extra information that you didn't need to know to solve the problem, but hopefully it helps you to understand what the equation is trying to tell you better.
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Since the velocity has opposite directions in different time moments, the question "when the velocity is maximal ?"
has NO much sense (if any). Much more reasonable question is "when the magnitude of the velocity is maximal ?"
1. Maximum velocity magnitude is when 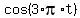 = +/- 1, i.e. when = +/- 1, i.e. when
 = =  ,
where "k" is any integer. First such a moment happens when k = 0, t = 0.
At this time moment velocity is -3 feet per second, and the velocity magnitude is 3 feet per second.
Next such a moment happens when t = ,
where "k" is any integer. First such a moment happens when k = 0, t = 0.
At this time moment velocity is -3 feet per second, and the velocity magnitude is 3 feet per second.
Next such a moment happens when t =  of a second.
At this time moment velocity is 3 feet per second, and the velocity magnitude is again 3 feet per second.
2. In the highest position the vertical velocity is equal to 0 (zero).
In the lowest position the vertical velocity is equal to 0 (zero), again.
It happens if and only if of a second.
At this time moment velocity is 3 feet per second, and the velocity magnitude is again 3 feet per second.
2. In the highest position the vertical velocity is equal to 0 (zero).
In the lowest position the vertical velocity is equal to 0 (zero), again.
It happens if and only if 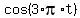 = 0, i.e. = 0, i.e.  = =  , or t = , or t = 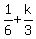 , where k is any integer.
Two such sequential time moments are t = , where k is any integer.
Two such sequential time moments are t =  of a second and t = of a second and t = 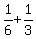 = =  of a second with the difference between them of of a second with the difference between them of  seconds. seconds.
|
|
|