Question 1076712: Please show me how to solve the triangle of B = 130°, c = 10.1, b = 5.2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! That is an impossible triangle.
Maybe there is a typo.
Otherwise, you are expected to say that the triangle is impossible.
You know that in any triangle,
a longer side is opposite a larger angle.
In the problem you posted, 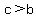 , ,
so for the angles, it should be 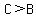 , ,
but  , so the triangle cannot have another larger angle. , so the triangle cannot have another larger angle.
IN GENERAL:
When a triangle is not a right triangle, you can use
Law of sines (easier if applicable) or
Law of cosines.
You know that in a triangle
the largest angle is the one opposite the longest side.
Law of done goes further and tells you that
the sine of an angle is proportional to the length of the opposite side.
As a formula, you can write it as
 or or  . .
If you have the measure of one angle (such as C),
and the length of the opposite side (such as c),
along with one other measurement of the triangle (such as b),
you can use Law of sines.
In that case,

would allow you to calculate the approximate value for
 . .
In general, the value for the 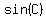 you found you found
could correspond to an acute angle,
or to the supplementary obtuse angle.
There are some cases where the answers would be two triangles.
However, there can be at most one obtuse angle.
|
|
|