SOLUTION: Solve the equation sin⁡θ=1−3cos⁡θ for all positive values of θ less than 360∘. Give the answers to three significant digits in the order of

Algebra ->  Test  -> Lessons -> SOLUTION: Solve the equation sin⁡θ=1−3cos⁡θ for all positive values of θ less than 360∘. Give the answers to three significant digits in the order of       Log On


   

Question 1068831: Solve the equation sin⁡θ=1−3cos⁡θ for all positive values of θ less than 360∘. Give the answers to three significant digits in the order of increasing.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
sin%28theta%29=1-3cos%28theta%29
Squaring both sides of the equal sign
could make us gain some extraneous solutions,
but at least we would not lose solutions.
Let's solve
sin%5E2%28theta%29%29=%281-3cos%28theta%29%29%5E2
1-cos%5E2%28theta%29=%281-3cos%28theta%29%29%5E2
1-cos%5E2%28theta%29=1-6cos%28theta%29%2B9cos%5E2%28theta%29
That is too much to write,
so I will call cos%28theta%29 x instead.
So, with the change of variable x=cos%28theta%29 ,
the equation is
1-x%5E2=1-6x%2B9x%5E2 .
I'm solving that for x .
1-x%5E2=1-6x%2B9x%5E2
1-x%5E2%2Bx%2A2-1=1-6x%2B9x%5E2%2Bx%2A2-1
0=-6x%2B10x%2A2
2x%285x-3%29=0--->system%28x=0%2C%22or%22%2C5x-3=0%29--->system%28x=0%2C%22or%22%2Cx=3%2F5%29
Both of those values are reasonable values for a cosine,
so I keep working with
system%28cos%28theta%29=0%2C%22or%22%2Ccos%28theta%29=3%2F5%29 .
I am on the way to find all solutions of the original equation plus some extraneous solutions.
I will have to check all solutions to find the good ones.
For "all positive values of theta less than 360%5Eo ,
or 0%3Ctheta%3C360%5Eo ,
cos%28theta%29=0 translates into system%28theta=90%5Eo%2C%22or%22%2Ctheta=270%5Eo%29 .
When theta=90%5Eo , sin%28theta%29=1 .
To check this solution,
I substitute theta=90%5Eo , or system%28sin%28theta%29=1%2Ccos%28theta%29=0%29 ,
into the original equation sin%28theta%29=1-3cos%28theta%29 .
to get 1=-3%2A0 , which is true,
so highlight%28matrix%281%2C6%2Ctheta%2C%22=%22%2C%229%22%2C%220%22%2C%22.%22%2C0%5Eo%29%29 is one of the solutions.
When theta=270%5Eo , sin%28theta%29=-1 ,
and that is not 1-3cos%28270%5Eo%29=1-3%2A0=1 , so theta%3C%3E270%5Eo .
That was an extraneous solution.
When cos%28theta%29=3%2F5 ,
sin%5E2%28theta%29=1-cos%5E2%28theta%29=1-%283%2F5%29%5E2=1-9%2F25=16%2F25=%284%2F5%29%5E2 ,
and 1-3cos%28theta%29=1-3%283%2F5%29=1-9%2F5=-4%2F5 ,
so we are looking for a 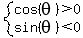theta with system%28cos%28theta%29%3E0%2Csin%28theta%29%3C0%29
According to my calculator, cos%28theta%29=3%2F5%29 happens when
theta=53.1%5Eo(rounded to 3 significant digits).
That is an extraneous solution, because that angle has 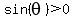sin%28theta%29%3E0 ,
so and 360%5Eo ,
there is one other angle with cos%28theta%29=3%2F5 .
It is theta=360%5E-53.1%5Eo=306.9%5Eo .
That is a solution of the original equation, and
"to three significant digits" it is highlight%28theta=307%5Eo%29 .
So, the solution to enter online as the answer,
"to three significant digits in the order of increasing" is
highlight%28matrix%281%2C6%2C9%2C0%2C%22.%22%2C0%5Eo%2C%22%2C%22%2C307%5Eo%29%29