Question 1046925: how do i solve for a vertex? when it asks for a Vertex of (0,0) and it is mimnimum?
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Depending how you have the equation, general form y=ax^2+bx+c or standard form y=a(x-h)^2+k;  will make vertex to be a minimum. Vertex of (0,0) will make the standard form equation take the format y=ax^2. The vertex would be the point, (h,k). will make vertex to be a minimum. Vertex of (0,0) will make the standard form equation take the format y=ax^2. The vertex would be the point, (h,k).
 is a reference equation for a parabola. Vertex will be the point (0,0). Setup a data table to find some point, graph the points, and sketch this and you will find a graph like this: is a reference equation for a parabola. Vertex will be the point (0,0). Setup a data table to find some point, graph the points, and sketch this and you will find a graph like this:

If you shift the graph leftward or rightward, using subtraction of some value h, then in standard form, you would have an equation like  . This would be a shift TO THE RIGHT, IF . This would be a shift TO THE RIGHT, IF 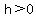 ; or a SHIFT TO THE LEFT IF ; or a SHIFT TO THE LEFT IF  . This means that the vertex, still touching the x-axis, will be at (h,0). . This means that the vertex, still touching the x-axis, will be at (h,0).
-
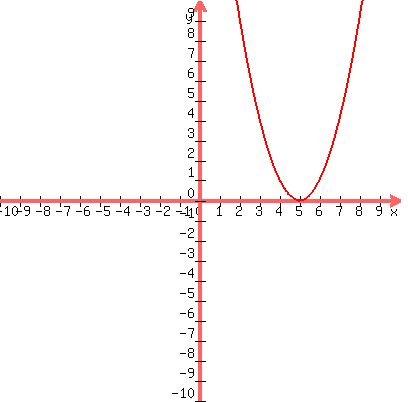
Imagine that h=5.
The equation could become  and the graph is this: and the graph is this:
Imagine that h=-2.
The equation could become  , or , or  and this shifts the model reference graph two units LEFTWARD, still with vertex touching the x-axis. and this shifts the model reference graph two units LEFTWARD, still with vertex touching the x-axis.
The graph:
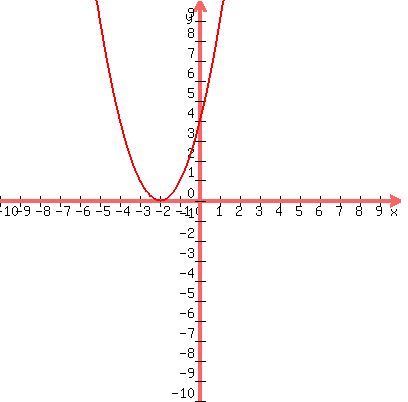 . .
and vertex is at (-2,0).
Looking again at standard form,  , and not yet discussing how k value will contribute to the shifting of the graph, vertex is (h,k); and if the vertex is (0,0), the Origin, then putting these coordinates values into the standard form model, , and not yet discussing how k value will contribute to the shifting of the graph, vertex is (h,k); and if the vertex is (0,0), the Origin, then putting these coordinates values into the standard form model,  , which simplifies to , which simplifies to  . .
I have used in these examples, a=1.
|
|
|