Tutors Answer Your Questions about test (FREE)
Question 1210384: If a+b+c=0
Then find (a²+b²+c²)/(b²-ac)
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1210375: If log₅2 = x and log₅3 = y,
find log₄₅100 in terms of x and y.
Found 2 solutions by mccravyedwin, math_tutor2020:
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Question 1210371: Candidates Q, R, and T are allowed to solve an advanced level Physics question independently. The probability that Q solves the question is 9/10, R solves the question is 3/7, and T solves the question is x.
(a) If the probability that at least one candidate solves the question is 19/70, find the value of x.
(b) Find the probability that:
(i) At least one candidate solves the question.
(ii) At most one candidate solves the question.
Found 4 solutions by Edwin McCravy, mccravyedwin, ikleyn, math_tutor2020:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'm thinking that you may have typed 19/70 when it should have been 69/70.
Candidates Q, R, and T are allowed to solve an advanced level Physics question
independently. The probability that Q solves the question is 9/10, R solves the
question is 3/7, and T solves the question is x.
(a) If the probability that at least one candidate solves the question is
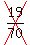  , find the value of x.
The probability that at least one candidate solved it is 1 minus the probability
that no candidate solved it, which is , find the value of x.
The probability that at least one candidate solved it is 1 minus the probability
that no candidate solved it, which is
  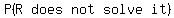   
 This must equal 1-69/70 or 1/70
This must equal 1-69/70 or 1/70




 <-- the value of x, which is the probability that T solves it.
>>>(i) At least one candidate solves the question.
Now, I do have to wonder why you asked this, since you gave it as <-- the value of x, which is the probability that T solves it.
>>>(i) At least one candidate solves the question.
Now, I do have to wonder why you asked this, since you gave it as 19/70 and I
changed it to 69/70.
The answer, of course is 69/70. LOL
>>>(ii) At most one candidate solves the question.
That's the probability that exactly one solved it or exactly none solved it.
case Q R T
1 Y N N (9/10)(1-3/7)(1-3/4) = (9/10)(4/7)(1/4) = 9/70
2 N Y N (1-9/10)(3/7)(1-3/4) = (1/10)(3/7)(1/4) = 3/280
3 N N Y (1-9/10)(1-3/7)(3/4) = (1/10)(4/7)(3/4) = 3/70
4 N N N (1-9/10)(1-3/7)(1-3/4) = (1/10)(4/7)(1/4) = 1/70
Sum those 4 fractions and get 11/56.
Edwin
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Candidates Q, R, and T are allowed to solve an advanced level Physics question independently.
The probability that Q solves the question is 9/10, R solves the question is 3/7, and T solves the question is x.
(a) If the probability that at least one candidate solves the question is 19/70, find the value of x.
(b) Find the probability that:
(i) At least one candidate solves the question.
(ii) At most one candidate solves the question.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
My dear visitor,
the problem in your post is posed INCORRECTLY.
Indeed, if the probability for Q to solve the problem is 9/10,
then the probability that "at least one candidate" will solve the problem
MUST BE AT LEAST 9/10.
But in your post the probability that at least one candidate will solve the problem is given as 19/70,
which makes no sense, contradicts to common sense and kills the problem to the death, instantly.
My condolences.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
P(Q) = probability that candidate Q solves the question
P(Q or R or T) = probability that at least one candidate solves the question
Use the inclusion-exclusion principle to say the following:
P(Q or R or T) = P(Q) + P(R) + P(T) - P(Q and R) - P(Q and T) - P(R and T) + P(Q and R and T)
P(Q or R or T) = P(Q) + P(R) + P(T) - P(Q)*P(R) - P(Q)*P(T) - P(R)*P(T) + P(Q)*P(R)*P(T)
P(Q or R or T) = 9/10 + 3/7 + x - (9/10)*(3/7) - (9/10)*x - (3/7)*x + (9/10)*(3/7)*x
P(Q or R or T) = (2x+33)/35
Set this equal to 19/70 and solve for x.
Doing so will lead to x = -47/4 = -11.75, but this is not a valid result since x must be in the interval from 0 to 1.
A probability of -11.75 makes no sense.
It appears some of the given probability values are flawed.
You'll need to contact your teacher for clarification.
Or perhaps there's something I might be overlooking.
Another way to arrive at this x value.
P(Q') = probability that Q fails to solve the question
P(Q') = 1 - P(Q) = 1 - 9/10
P(Q'R'T') = probability all 3 people fail
P(Q'R'T') = P(Q')*P(R')*P(T')
P(Q'R'T') = (1-9/10)*(1-3/7)*(1-x) = 1-19/70
(1-9/10)*(1-3/7)*(1-x) = 1-19/70
Solving that equation should lead you to x = -47/4 = -11.75
Notice that the events "at least one solves the question" and "all 3 fail to solve" are complementary events.
One or the other must happen.
This complementary nature is why we're allowed to subtract the probabilities from 1.
Question 1210363: A cone has a radius of 10cm and slant height of 26cm. find the volume of the cone
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A cone has a radius of 10cm and slant height of 26cm. find the volume of the cone
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill, giving the answer 3117.85 cm^3, is incorrect.
Below is my correct solution.
The height of the cone is h =  = = 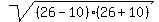 = =  = 4*6 = 24 cm to calculate it mentally.
The volume of the cone is V = = 4*6 = 24 cm to calculate it mentally.
The volume of the cone is V =  = =  = 3.14159*100*8 = 2513.27 cm^3. ANSWER = 3.14159*100*8 = 2513.27 cm^3. ANSWER
Solved correctly.
===============================
The problem is elementary simple and routine, and my correct solution was in two lines.
The incorrect gibberish by @CPhill barely fit 30 lines.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solutions are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the volume of the cone:
**1. Understand the Formulas**
To find the volume of a cone, you need its radius ($r$) and its height ($h$). The formula for the volume of a cone is:
$V = \frac{1}{3} \pi r^2 h$
You are given the radius ($r = 15 \text{ cm}$) and the slant height ($l = 20 \text{ cm}$), but you need to find the height ($h$).
**2. Find the Height (h)**
The radius, height, and slant height of a cone form a right-angled triangle, with the slant height as the hypotenuse. We can use the Pythagorean theorem:
$r^2 + h^2 = l^2$
Substitute the given values:
$15^2 + h^2 = 20^2$
$225 + h^2 = 400$
$h^2 = 400 - 225$
$h^2 = 175$
$h = \sqrt{175}$
To simplify $\sqrt{175}$:
$175 = 25 \times 7$
$h = \sqrt{25 \times 7} = 5\sqrt{7} \text{ cm}$
**3. Calculate the Volume (V)**
Now that you have the height, plug the values of $r$ and $h$ into the volume formula:
$V = \frac{1}{3} \pi r^2 h$
$V = \frac{1}{3} \pi (15)^2 (5\sqrt{7})$
$V = \frac{1}{3} \pi (225) (5\sqrt{7})$
$V = 75 \pi (5\sqrt{7})$
$V = 375\sqrt{7}\pi \text{ cm}^3$
**4. Approximate the Value (Optional)**
If you need a numerical approximation, use $\pi \approx 3.14159$ and $\sqrt{7} \approx 2.64575$:
$V \approx 375 \times 2.64575 \times 3.14159$
$V \approx 992.15625 \times 3.14159$
$V \approx 3117.85 \text{ cm}^3$
The exact volume of the cone is $375\sqrt{7}\pi \text{ cm}^3$.
Approximately, the volume is $3117.85 \text{ cm}^3$.
Question 1164845: Determine the present value of a series of 30 quarterly payments of $3,500 each which begins one month from today. Assume interest of 8.25 percent per year compounded monthly
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine the present value of a series of 30 quarterly payments of $3,500 each,
which begins one month from today. Assume interest of 8.25 percent per year compounded monthly.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this tricky problem, we have quarterly payments of $3,500 each compounded monthly,
and the payments begin one month from today.
We are going to consider it as an Annuity Due saving plan, which starts one month from today.
But as given, in this problem the compounding is desynchronized with the payments.
There is a standard formula for the Future Value of an Annuity Due saving plan, but this formula
was derived for synchronized payments and compounding.
Therefore, we want synchronize payments and compounding.
To synchronize them, we will introduce an equivalent effective quarterly compounding coefficient
expressing it via the monthly compounding coefficient
c = 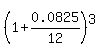 = 1.020767122.
Thus we will consider an equivalent scheme with quarterly compounding, synchronized with quarterly payments/deposits.
Then the Future Value of this equivalently modified account after 30 quarterly payments is calculated
using the standard formula for Annuity Due saving plan
FV = = 1.020767122.
Thus we will consider an equivalent scheme with quarterly compounding, synchronized with quarterly payments/deposits.
Then the Future Value of this equivalently modified account after 30 quarterly payments is calculated
using the standard formula for Annuity Due saving plan
FV =  dollars.
But remember that this formula gives the Future Value of the Annuity Due at the end
of the Annuity Due saving plan, which happens 3 months after the last payment.
We, in opposite, want to know the amount of the account at the time of the last payment,
i.e. 3 months before the end of the Annuity Due saving plan.
It makes clear, that to calculate the amount A(30) at the account at the last, 30-th payment,
we should use the formula
A(30) = dollars.
But remember that this formula gives the Future Value of the Annuity Due at the end
of the Annuity Due saving plan, which happens 3 months after the last payment.
We, in opposite, want to know the amount of the account at the time of the last payment,
i.e. 3 months before the end of the Annuity Due saving plan.
It makes clear, that to calculate the amount A(30) at the account at the last, 30-th payment,
we should use the formula
A(30) =  = = 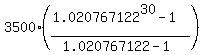 = 143706.81 dollars.
Now we want to find the present value X. It is the starting value of the other account (one-time deposit),
which, when compounded monthly at 8.25% per year, will generate the same value
at the time of the 30-th payment, i.e. after 29 quarters PLUS 1 month = 3*29 + 1 = 88 months.
So, we write this equation
143706.81 = = 143706.81 dollars.
Now we want to find the present value X. It is the starting value of the other account (one-time deposit),
which, when compounded monthly at 8.25% per year, will generate the same value
at the time of the 30-th payment, i.e. after 29 quarters PLUS 1 month = 3*29 + 1 = 88 months.
So, we write this equation
143706.81 =  .
It gives the solution
X = .
It gives the solution
X =  = 78637.24 dollars.
ANSWER. The present value is $78,637.24. = 78637.24 dollars.
ANSWER. The present value is $78,637.24.
Solved.
Question 1210359: The dimensions of a square is given as 6.25 cm. A student measured one side of the square as 6.12 cm to calculate the perimeter and the area of the square.
Find the percentage error in:
i. Measured length
ii. Calculated perimeter
iii. Calculated area
Found 4 solutions by mccravyedwin, ikleyn, Edwin McCravy, MathLover1:
Answer by mccravyedwin(405)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In case you are studying what I think you are, and not a 6 grader, here are some
links:
Calculus - Differentials with Relative and Percent Error
https://www.youtube.com/watch?v=4DuQh5oUsbQ
Differentials: Propagated Error
https://www.youtube.com/watch?v=6u-ldWJKN7A
Edwin
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The dimensions of a square is given as 6.25 cm. A student measured one side of the square as 6.12 cm to calculate
the perimeter and the area of the square. Find the percentage error in:
i. Measured length
ii. Calculated perimeter
iii. Calculated area
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is a standard 6-grade exercise for ratio and percentage.
Therefore, I solve it at the appropriate level using elementary algebra
with complete explanations and without involving other approaches.
In this problem, we are given the precise value of the side of the square as 6.25 cm,
and we also are given some measured value of the side of the square,
which represents some deviation from the precise value.
For part (iii), we should calculate the deviation as the difference
measured value  the precise value. (1)
In this case, we have no measured value for the area, but we can compute it as the square
of the measured side, 6.12^2 cm^2.
So, doing it in the course of formula (1), we calculate the deviation of the computed area as
computed area 6.12^2 cm^2 MINUS the precise area 6.25^2 cm^2, or 6.12^2 - 6.25^2 = -1.6081 cm^2.
Then we relate this found deviation of the area to the EXACT GIVEN value of the area.
Doing this way, we obtain the precise value. (1)
In this case, we have no measured value for the area, but we can compute it as the square
of the measured side, 6.12^2 cm^2.
So, doing it in the course of formula (1), we calculate the deviation of the computed area as
computed area 6.12^2 cm^2 MINUS the precise area 6.25^2 cm^2, or 6.12^2 - 6.25^2 = -1.6081 cm^2.
Then we relate this found deviation of the area to the EXACT GIVEN value of the area.
Doing this way, we obtain
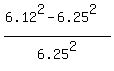 = -0.04116736 = -0.041167 (rounded), or -4.1167%.
The sign " minus " here points that the measured/computed area is less than the precise value.
But since the problem asks about the " error ", it instructs us to take the absolute value
of the calculated "percentage of the deviation".
So, the correct answer for (iii) is 4.1167% (the positive value). = -0.04116736 = -0.041167 (rounded), or -4.1167%.
The sign " minus " here points that the measured/computed area is less than the precise value.
But since the problem asks about the " error ", it instructs us to take the absolute value
of the calculated "percentage of the deviation".
So, the correct answer for (iii) is 4.1167% (the positive value).
Solved.
------------------------------
Notice that in such problems, choosing and using a correct treatment
is of a principial importance, and it does not allow to split or to double or to modify the interpretation.
The whole wisdom in solving such problems is that if the precise value is given,
then we should calculate the percentage of the deviation using the formulas centered around this precise given value;
then we should take the absolute value for the final " error value ".
Thus, in accordance with the problem intention/purpose, this my post TEACHES you
to interpret the problem correctly at the 6-grade level, and also TEACHES you to choose and to use
ONE single UNIQUE CORRECT interpretation for this level
and work with it /(follow it) it from the beginning to the end.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1210358: A factory has 80 employees. If the number of men is doubled and the women tripled, the staff strength would be 190. Find the initial number of men and women working in the factory.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor has provided a typical formal mathematical solution to the problem.
To see that the formal mathematics only formalizes common sense and logical reasoning, here is an informal solution that follows exactly the same computational path as the formal solution provided by the other tutor.
The original number of employees was 80.
If the numbers of both men and women were doubled, the total number of employees would be 80*2 = 160.
But if the number of men was doubled and the number of women was tripled, the new total number of employees would be 190.
That difference of 30 between 190 and 160 is because the number of women was tripled instead of doubled.
That means the original number of women was 30.
And that means the original number of men was 80-30 = 50.
ANSWERS: 30 women and 50 men.
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A factory has 80 employees. If the number of men is doubled and the women tripled,
the staff strength would be 190. Find the initial number of men and women working in the factory.
~~~~~~~~~~~~~~~~~~~~~~~~~
Let m be the number of men the factory has.
Let w be the number of women the factory has.
Write equations as you red the problem
m + w = 80, (1)
2m + 3w = 190. (2)
To solve this system of equations, multiply equation (1) by 2;
keep equation (2) as is
2m + 2w = 160, (3)
2m + 3w = 190. (4)
Now subtract equation (3) from equation (2). You will get
3w - 2w = 190 - 160
w = 30.
Thus the number of women is 30.
The number of men is 80-30 = 50.
Solved.
Come again to get help.
Question 1167519: Help is super appreciated!
At noon, ship A is 130 km west of ship B. Ship A is sailing east at 30 km/h and ship B is sailing north at 25 km/h. How fast is the distance between the ships changing at 4:00 PM?
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At noon, ship A is 130 km west of ship B. Ship A is sailing east at 30 km/h
and ship B is sailing north at 25 km/h. How fast is the distance between the ships changing at 4:00 PM?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In a coordinate plane (x.y), ship A and ship B are in the coordinate line "west - east" initially.
In standard notations, this coordinate line is horizontal y = 0.
For ship A, its initial coordinate is (-130,0).
For ship B, its initial coordinate is (0,0).
In 4 hours, at 4:00 pm, ship A is at the point (-10,0),
while ship B is at the point (0,100).
The distance between the ships at t= 4:pm is
D0 =  = =  = =  .
The parametric form of the path for ship A is (-10 + 30t, 0);
for ship B (0, 100 + 25t),
where 't' is the time after 4:00 pm.
The square of the distance between the ships in parametric form is
D^2(t) = (-10+30t)^2 + (100+25t)^2.
Take the time derivative of both sides, considering D^2(t) as a composite function .
The parametric form of the path for ship A is (-10 + 30t, 0);
for ship B (0, 100 + 25t),
where 't' is the time after 4:00 pm.
The square of the distance between the ships in parametric form is
D^2(t) = (-10+30t)^2 + (100+25t)^2.
Take the time derivative of both sides, considering D^2(t) as a composite function
 = 2*(-10)*30 + 2*100*25.
Simplify = 2*(-10)*30 + 2*100*25.
Simplify
 = 4400
and find the rate of the distance change between the ships = 4400
and find the rate of the distance change between the ships
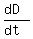 = = 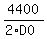 = =  = 21.891 km/h (rounded). <<<---=== ANSWER = 21.891 km/h (rounded). <<<---=== ANSWER
At this point, the solution is complete.
Question 1167520: I'm really struggling with this. Please help me out! (Not actually a test problem: This is Calc.)
A plane flies horizontally at an altitude of 6 km and passes directly over a tracking telescope on the ground. When the angle of elevation is π/3, this angle is decreasing at a rate of π/3 rad/min. How fast is the plane traveling at that time?
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1165804: A transportation company is interested in knowing the amount of time it takes for the different type of vehicles they own to travel certain distances based on their different speeds. A car travels 180 miles in the same time that a truck travels 120 miles. If the car’s speed is 20 miles per hour faster than the truck’s, find the car’s speed and the truck’s speed. Make sure to show all your work.
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1210348: x, y, z ∈ Z³
13/x² + 1996/y² = z/1997
x, y, z = ?
Found 4 solutions by AnlytcPhil, ikleyn, mccravyedwin, Edwin McCravy:
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1210348
I kept on using the same technique, trying powers of 2 for x and y and
found all these solutions, and corrected the one I mis-punched my
calculator on.
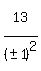  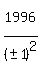  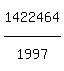   (x,y,z) = (1,1,1422464), (1,-1,1422464), (-1,1,1422464), (-1,-1,1422464).
These others give 4 solutions in the same way:
(x,y,z) = (1,1,1422464), (1,-1,1422464), (-1,1,1422464), (-1,-1,1422464).
These others give 4 solutions in the same way:
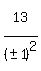  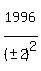      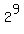
  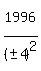      
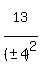  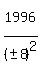      
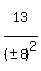        
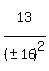    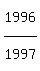    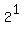 So, except for the 1st solution above, we could generalize on the others this
way. Maybe Ikleyn can prove this generalization for them:
So, except for the 1st solution above, we could generalize on the others this
way. Maybe Ikleyn can prove this generalization for them:
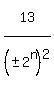    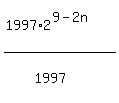  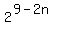 for n = 0,1,2,3,4
But I'm still not sure there are any other solutions. I said I was sure I had
all of them before, and then found these and had to eat my words. LOL
Edwin
for n = 0,1,2,3,4
But I'm still not sure there are any other solutions. I said I was sure I had
all of them before, and then found these and had to eat my words. LOL
Edwin
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x, y, z ∈ Z³
13/x² + 1996/y² = z/1997
x, y, z = ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will list below two families of  solutions in solutions in  numbers (x,y,z). numbers (x,y,z).
(a) (x,y) = (+/-1, +/-1) ---> z = (13+1996)*1997 = 4011973. 4 solutions.
(b) (x,y) = (+/-1, +/-2) ---> z = (13+499)*1997 = 1022464. 4 solutions.
Why they are the solutions - it is obvious: it is enough to look at denominators.
I don't know if where are other solutions.
Edwin correctly recognized and pointed 4 solutions of family (a).
Edwin made an error pointing other 4 his solutions.
In my notations, they are 4 solutions (b), with (or after) my correction.
/////////////////////////////////////////////
Here is an addition to the set of solutions found by Edwin
(x,y,z) = (+/-7, +/-7, 81877).
Indeed, left side of the original equation is  + +  = =  = =  = 41, = 41,
and right side is 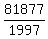 = 41. = 41.
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Since 1996 is divisible by perfect squares 1 and 4, let
y2 = ± either of these.
Since 1996 is divisible by perfect squares 1 and 4, let
y2 = ± either of these.
 , and where y2 = 1 or 4 , and where y2 = 1 or 4


 For
For  , ,


 So that gives these solutions
(x,y,z) = (1,1,4011973), (1,-1,4011973), = (-1,1,4011973), = (-1,-1,4011973)
For
So that gives these solutions
(x,y,z) = (1,1,4011973), (1,-1,4011973), = (-1,1,4011973), = (-1,-1,4011973)
For  , ,


 So that gives these solutions
(x,y,z) = (1,2,2018967), (1,-2,2018967), = (-1,2,2018967), = (-1,-2,2018967)
in addition to these we already found:
(x,y,z) = (1,1,4011973), (1,-1,4011973), (-1,1,4011973), (-1,-1,4011973)
I doubt there are any other solutions besides these 8, but I don't know that for
sure.
Maybe another tutor can find others or show that there are no others.
Edwin
So that gives these solutions
(x,y,z) = (1,2,2018967), (1,-2,2018967), = (-1,2,2018967), = (-1,-2,2018967)
in addition to these we already found:
(x,y,z) = (1,1,4011973), (1,-1,4011973), (-1,1,4011973), (-1,-1,4011973)
I doubt there are any other solutions besides these 8, but I don't know that for
sure.
Maybe another tutor can find others or show that there are no others.
Edwin
Question 1210351: Find the exact value of
tan⁸40° - 36tan⁶40° + 126tan⁴40 - 84tan²40
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1210352: x^logy + y^logx = 2
x^logx + y^logy = 11
find x = ?, y = ?
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x^logy + y^logx = 2
x^logx + y^logy = 11
find x = ?, y = ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
One solution is x = 10, y = 1.
Another solution is x = 1, y = 10.
The method of finding the solutions is trial and error.
To check the solutions validity, substitute the values into equations.
Question 1210347: x/y = a/b = 2/3
y² - b² = 27
x² - a² = ?
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1210346: Solve for x,
π⁴ˣ - 10π²ˣ + 9 = 0
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1209804: If sinx + sin²x + sin³x = 1,
find cos⁶x - 4cos⁴x + 8cos²x
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1177476: There are 150 people at an International
Medical Conference. 40 are Africans, 70
are women and 110 are doctors. 12 of the
women are Africans, 46 of the doctors are
women and 31 of the Africans are doctors.
If 5 of the African men are not doctors:
a how many of the African women are
doctors
b how many of the men are neither African
nor doctors?
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are 150 people at an International Medical Conference.
40 are Africans, 70 are women and 110 are doctors.
12 of the women are Africans, 46 of the doctors are women and 31 of the Africans are doctors.
If 5 of the African men are not doctors:
(a) how many of the African women are doctors ?
(b) how many of the men are neither African nor doctors?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, his solution to part (a) is OUT of LOGIC, so it is INCORRECT.
Below is my solution for part (a).
(a) How many of the African women are doctors ?
The solution is in 3 logical steps.
(1) We are given that there are 40 Africans, and 12 of women are Africans.
Hence, the number of African men is 40-12 = 28.
(2) Next, we are given that 5 of African men are not doctors.
Hence, 28-5 = 23 is the number of African men who are doctors.
(3) Next, we are given that 31 of Africans are doctors.
Hence, the number of African women who are doctors is 31-23 = 8.
ANSWER. The number of African women who are doctors is 8.
Part (a) is solved.
Question 1210339: In ∆ PQR, │PQ│= 9cm, │QR│= 11cm, │RP│= 7cm and the bisector of ln ∠P meets line QR at T. Calculate │QT│ and│TR│.
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1210334: The following are the marks scored by 20 students in a test:
15 11 17 25 13 15 16 22 24 27
20 22 15 16 15 19 22 24 22 11
(a) Prepare a frequency table for the distribution using class intervals 10 - 12, 13 - 15, 16-18....
(b) Calculate the variance of the distribution.
(c) If the pass mark for the test was 16, find the probability that a student selected at random from the class failed.
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Question 1210335: A tower TR and an observer at O. |OR| = 84 m and the angle of elevation of the top of the tower T from O is 57°.
(a) Calculate, correct to three significant figures, the height of the tower.
(b) The observer at O, moved away from the tower in the same straight line until the angle of elevation of T is 49°. Find, correct to two decimal places, how far the observer moved backwards.
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A tower TR and an observer at O. |OR| = 84 m and the angle of elevation of the top of the tower T from O is 57°.
(a) Calculate, correct to three significant figures, the height of the tower.
(b) The observer at O, moved away from the tower in the same straight line until the angle of elevation of T is 49°.
Find, correct to two decimal places, how far the observer moved backwards.
~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, 'T' denotes the top of the tower; 'R' denotes its base.
(a) In part (a), we have a right-angled triangle with vertical leg |TR| and horizontal leg |OR| = 84 m.
Recall the definition of tangent of an acute angle in a right-angled triangle
opposite leg
 = ---------------.
adjacent leg
In this part, the angle is 57°, the opposite leg is the unknown height of the tower h = |TR|,
the adjacent leg is the given horizontal distance from the observer to the base of the tower |OR| = 84 m.
So, we write
tan(57°) = = ---------------.
adjacent leg
In this part, the angle is 57°, the opposite leg is the unknown height of the tower h = |TR|,
the adjacent leg is the given horizontal distance from the observer to the base of the tower |OR| = 84 m.
So, we write
tan(57°) =  .
From this equation, the height of the tower 'h' is
h = |OR|*tan(57°) = 84*1.53986496381 = 129.35 m (rounded).
Thus the height of the tower is 129.35 m. ANSWER
(b) In part (b), we have a right-angled triangle with vertical leg |TR| = h = 129.35 m and horizontal leg x,
where x is the new horizontal distance from the observer to the base of the tower.
Using the definition of the tangent of an acute angle in a right-angled triangle, we can write
tan(49°) = .
From this equation, the height of the tower 'h' is
h = |OR|*tan(57°) = 84*1.53986496381 = 129.35 m (rounded).
Thus the height of the tower is 129.35 m. ANSWER
(b) In part (b), we have a right-angled triangle with vertical leg |TR| = h = 129.35 m and horizontal leg x,
where x is the new horizontal distance from the observer to the base of the tower.
Using the definition of the tangent of an acute angle in a right-angled triangle, we can write
tan(49°) =  .
From this equation, the new distance from the tower to the observer is
x = .
From this equation, the new distance from the tower to the observer is
x =  = = 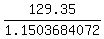 = 112.44 m (rounded).
It means that the observer moved backward 112.44 - 84 = 28.44 meters. ANSWER = 112.44 m (rounded).
It means that the observer moved backward 112.44 - 84 = 28.44 meters. ANSWER
Solved.
Question 1210336: (a) The eighth term of an Arithmetic Progression (A.P) is 46 and the sum of the first eight terms is 200. Find the:
(i) first term;
(ii) sum of the first 12 terms.
(b) The points X(70°S, 60°E) and Y(7°S, 60°E) lies on the surface of the earth.
(i) Illustrate the information in a diagram.
(ii) Find the distance between X and Y along the meridian.
[Take л = 22/7 and R = 6,400 km]
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(b) The points X(70°S, 60°E) and Y(7°S, 60°E) lies on the surface of the earth.
(i) Illustrate the information in a diagram.
(ii) Find the distance between X and Y along the meridian.
[Take л = 22/7 and R = 6,400 km]
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Calculations in the post by @greenestamps, giving the answer of 3520 km, are erroneous.
From the school, we know that the Earth circumference along the equator
is about 40,000 kilometers.
In this problem, we consider the Earth as spherical; so, its circumference
in any meridional section is the same 40,000 km.
Hence, under this assumption, the distance from the South pole to the North pole
along any meridian is half of 40,000 km, i.e. 20,000 km.
In this problem, the distance between the given points is 70° - 7° = 63°, measured as the difference of altitudes.
It is about one third of 180°, which represents the distance between the poles, expressed in degrees.
So, we can expect, that the distance between the given points is at least one third of 20,000 km.
i.e., at least 6666 km.
If you want to derive the value using the formula, you should write
 = =  = = 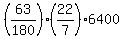 = = 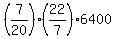 = = 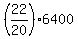 = 22*320 = 7040 kilometers. = 22*320 = 7040 kilometers.
It is the precise answer (under the given values and assumptions),
and it is consistent with my crude evaluation above.
---------------------------
Solved, with explanations.
Answer by greenestamps(13195)   (Show Source): (Show Source):
Question 1210333: A company installs solar panels in its premises to reduce its electricity cost. The monthly savings on electricity in $, is modelled by S=200+50x-2x², where x is the number of months after installation.
(a) At what time will the savings on electricity stop increasing?
(b) Find the maximum savings.
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A company installs solar panels in its premises to reduce its electricity cost.
The monthly savings on electricity in $, is modelled by S=200+50x-2x²,
where x is the number of months after installation.
(a) At what time will the savings on electricity stop increasing?
(b) Find the maximum savings.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The given quadratic function describes a parabola.
This parabola is opened downward, because the leading coefficient at x^2 is negative.
So, the parabola has a maximum at its vertex.
(a) the given quadratic function is increasing on the left of the vertex.
x-coordinate of the vertex is  , where 'a' = -2 is the coefficient at x^2
and 'b' = 50 is the coefficient at x. So, x-coordinate of the vertex is , where 'a' = -2 is the coefficient at x^2
and 'b' = 50 is the coefficient at x. So, x-coordinate of the vertex is
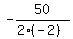 = = 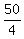 = 12.5.
For the further analysis, take into account that 'x' in this problem is, factually, not a continuous time,
but a discrete counter of months. The value of 12.5 is exactly half-way between 12 and 13.
Since the parabola is symmetric about the vertex coordinate, we round the time 12.5 months to 12 months.
It means that the monthly saving on electricity stops increasing at the 12-th month, according to the given data.
(b) To find the maximum monthly saving, calculate the value of the given quadratic function at x = 12.
The maximum monthly saving will be 200 + 50*12 - 2*12^2 = 512 dollars.
Below is the table showing monthly savings for the first 15 months calculated using the given formula.
The table confirms that the monthly payment increases till the month 12 and stops increasing then.
It also confirms that the maximum monthly payment is $512.
month monthly
saving
------------------------
1 248
2 292
3 332
4 368
5 400
6 428
7 452
8 472
9 488
10 500
11 508
12 512
13 512
14 508
15 500 = 12.5.
For the further analysis, take into account that 'x' in this problem is, factually, not a continuous time,
but a discrete counter of months. The value of 12.5 is exactly half-way between 12 and 13.
Since the parabola is symmetric about the vertex coordinate, we round the time 12.5 months to 12 months.
It means that the monthly saving on electricity stops increasing at the 12-th month, according to the given data.
(b) To find the maximum monthly saving, calculate the value of the given quadratic function at x = 12.
The maximum monthly saving will be 200 + 50*12 - 2*12^2 = 512 dollars.
Below is the table showing monthly savings for the first 15 months calculated using the given formula.
The table confirms that the monthly payment increases till the month 12 and stops increasing then.
It also confirms that the maximum monthly payment is $512.
month monthly
saving
------------------------
1 248
2 292
3 332
4 368
5 400
6 428
7 452
8 472
9 488
10 500
11 508
12 512
13 512
14 508
15 500
Solved.
Question 1210337: A sector of a circle of radius 6 cm subtends an angle of 105° at the centre. Calculate the:
(i) perimeter;
(ii) area;
of the sector.
[Take π = 22/7]
Answer by ikleyn(52751)   (Show Source): (Show Source):
Question 1210331: In a certain year, the consumption pattern of electricity charges in a town was as follows:
the cost of the first 30 units was $1.00 per unit;
the cost of the next 30 units was $7.00 per unit;
the cost of each additional unit was $5.00.
(a) If Amaka used 420 units of electricity in January that year, calculate the amount paid.
(b) If Amaka paid $2,740.00 in the month of February, calculate the number of units
of electricity consumed.
(c) Find, correct to two decimal places, the percentage change in units of electricity
consumed by Amaka in January and February.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52751)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a certain year, the consumption pattern of electricity charges in a town was as follows:
the cost of the first 30 units was $1.00 per unit;
the cost of the next 30 units was $7.00 per unit;
the cost of each additional unit was $5.00.
(a) If Amaka used 420 units of electricity in January that year, calculate the amount paid.
(b) If Amaka paid $2,740.00 in the month of February, calculate the number of units
of electricity consumed.
(c) Find, correct to two decimal places, the percentage change in units of electricity
consumed by Amaka in January and February.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, in part (c) they ask about the percentage change in units of electricity,
while @greenestamps calculated the percentage change in the cost.
So, a correct calculation for part (c) is
the percentage change in units of electricity = 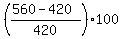 = =  = =  = 33.33% (rounded). ANSWER = 33.33% (rounded). ANSWER
----------------------
The post solution note
How the question is posed in part (c), it makes the request ambiguous,
since from this form it is UNCLEAR, which of the two months is considered as the base for the comparison.
In this sense, the question is mathematically DEFECTIVE.
In my calculation, I took the January consumption of electricity as the base for the comparison.
Had I create this problem, I would formulate part (c) differently
(c) Find, correct to two decimal places, the percentage change in units
of electricity, consumed by Amaka, from January to February.
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The cost of the first 60 units of electricity is 30($1) + 30($7) = $240.
(a) Amaka used 420 units in January. That means 420-60 = 360 units at $5 each, for an additional cost of 360($5) = $1800. The total amount paid in January was $240 + $1800 = $2040.
(b) In February, Amaka paid $2740 for electricity. The first 60 units cost $240, so the amount paid at $5 per unit was $2740-$240 = $2500. That means $2500/$5 = 500 units at that rate, making a total of 60+500 = 560 units for February.
(c) Amaka paid $2040 in January and $2740 in February. The percentage change is
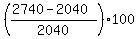
To two decimal places, that percentage change is 34.31.
ANSWERS:
(a) $2040
(b) 560 units
(c) 34.31%
Question 1210332:
Given that
P = │ 2 4 │
│-9 1 │
and
Q = │1 - 1│
│3 -2│,
find PQ + 2Q.
Found 3 solutions by math_tutor2020, MathLover1, mccravyedwin:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
There are two routes you can follow.- Compute PQ and 2Q separately. Then add them together. This is what tutor Edwin has done.
- Note that Q is present in both PQ and 2Q, so we can factor it out using the distributive property. PQ + 2Q = PQ + 2*I*Q = (P+2I)*Q. Where I is the identity matrix. Be careful to remember that matrix multiplication is NOT commutative.
I should elaborate on the 2nd method. The identity matrix is needed so that we can validly add the stuff in the parenthesis.
The expression P+2 wouldn't make much sense to add a matrix to a scalar.
But P+2I makes more sense because it's the expression  i.e. i.e. 
I'll let the student handle the scratch work for the second method if they follow that route.
You can use online calculators to verify that Edwin has the correct answer.
The tutor MathLover1 mistakenly computed 2P instead of PQ, so that explains why she arrived at an incorrect answer.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Question 1210324: The product of the ages of Adu and Tanko is 9 less than Akorfa's age. If Tanko is 4 years older than Adu and Akorfa's age is six times Tanko's age, find Akorfa's age.
Answer by mccravyedwin(405)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I agree with greenstamps. Sometimes I feel that we tutors are trying to show each
other how smart we are, by coming up with clever shorter ways to solve problems.
If we're doing that (and I won't say I'm not guilty of it myself!), we need to
stop it and stop it immediately! These students are struggling.
We need to try our damndest to figure out what methods these students are being
taught in class and use those same methods and none other.
Edwin
PS: Yes, I've been using online solvers. But I've heard that these are being used in schools these days.
I was teaching when calculators first came out. Many teachers would not allow
them. What they did was reduce arithmetic to a trivial process. Solvers are
now reducing algebraic manipulation to trivial in the same way. Where's it all
going? Damned if I know.
Edwin
Question 1210329: Yaro drove from a town Gaja to Banga. After 2 hours in the journey, he observed that he had covered 80 km and realized that if he continued driving at same average speed, he would end up being late for 15 minutes. If he decided to increase the average speed by 10 km/h, he would arrive at Banga 36 minutes earlier. Find the distance between Gaja and Banga.
Answer by greenestamps(13195)   (Show Source): (Show Source):
Question 1210327: YyThe data represent the scores obtained by 9 applicants in an interview arranged in
ascending order: (3x+2), 22, (4x-2), 23, 25, (5x-4), 29, 29 and (x²-7).
(a) Given that the range is 9, find the
(i) value of .x;
(ii) mean mark of the applicants.
(b) If four of the applicants who obtained the highest score were selected, determine the
pass mark.
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Start using the given information that the range is 9.




x = 6 or x = -3
But negative scores don't make sense, so x is 6. The scores are then
20, 22, 22, 23, 25, 26, 29, 29, and 29
The mean of the marks can of course be found by adding the 9 scores and dividing by 9.
But when finding the mean of a set of numbers that are all close together, another method is to guess the mean and look at the "overs" and "unders" compared to that guess.
Looking at the scores, it looks as if the mean is about 25. Comparing the 9 scores to that guess, we get
-5, -3, -3, -2, 0, 1, 4, 4, and 4
Adding those gives us -13+13 = 0, so in fact our guess of 25 for the mean is correct.
ANSWERS:
(a)(i) x = 6
(a)(ii) the mean score is 25
(b) the top 4 scores are 26, 29, 29, and 29, so the pass mark is 26
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955, 17956..18000, 18001..18045, 18046..18090, 18091..18135, 18136..18180, 18181..18225, 18226..18270, 18271..18315, 18316..18360, 18361..18405, 18406..18450, 18451..18495, 18496..18540, 18541..18585, 18586..18630, 18631..18675, 18676..18720, 18721..18765, 18766..18810, 18811..18855, 18856..18900, 18901..18945, 18946..18990, 18991..19035, 19036..19080, 19081..19125, 19126..19170, 19171..19215, 19216..19260, 19261..19305, 19306..19350, 19351..19395, 19396..19440, 19441..19485, 19486..19530, 19531..19575, 19576..19620, 19621..19665, 19666..19710, 19711..19755, 19756..19800, 19801..19845, 19846..19890, 19891..19935, 19936..19980, 19981..20025, 20026..20070, 20071..20115, 20116..20160, 20161..20205, 20206..20250, 20251..20295, 20296..20340, 20341..20385, 20386..20430, 20431..20475, 20476..20520, 20521..20565, 20566..20610, 20611..20655, 20656..20700, 20701..20745, 20746..20790, 20791..20835, 20836..20880, 20881..20925, 20926..20970, 20971..21015, 21016..21060, 21061..21105, 21106..21150, 21151..21195, 21196..21240, 21241..21285, 21286..21330, 21331..21375, 21376..21420, 21421..21465, 21466..21510, 21511..21555, 21556..21600, 21601..21645, 21646..21690, 21691..21735, 21736..21780, 21781..21825, 21826..21870, 21871..21915, 21916..21960, 21961..22005, 22006..22050, 22051..22095, 22096..22140, 22141..22185, 22186..22230, 22231..22275, 22276..22320, 22321..22365, 22366..22410, 22411..22455, 22456..22500, 22501..22545, 22546..22590, 22591..22635, 22636..22680, 22681..22725, 22726..22770, 22771..22815, 22816..22860, 22861..22905, 22906..22950, 22951..22995, 22996..23040, 23041..23085, 23086..23130, 23131..23175, 23176..23220, 23221..23265, 23266..23310, 23311..23355, 23356..23400, 23401..23445, 23446..23490, 23491..23535, 23536..23580, 23581..23625, 23626..23670, 23671..23715, 23716..23760, 23761..23805, 23806..23850, 23851..23895, 23896..23940, 23941..23985, 23986..24030, 24031..24075, 24076..24120, 24121..24165, 24166..24210, 24211..24255, 24256..24300, 24301..24345, 24346..24390, 24391..24435, 24436..24480, 24481..24525, 24526..24570, 24571..24615, 24616..24660, 24661..24705, 24706..24750, 24751..24795, 24796..24840, 24841..24885, 24886..24930, 24931..24975, 24976..25020, 25021..25065, 25066..25110, 25111..25155, 25156..25200, 25201..25245, 25246..25290, 25291..25335, 25336..25380, 25381..25425, 25426..25470, 25471..25515, 25516..25560, 25561..25605, 25606..25650
|



