All four sides of a rhombus have equal measures, so each side is  of the perimeter or
of the perimeter or 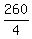 = 65. So we label the upper left side 65.
We are given that one of the diagonals is 66. Let that be the red diagonal
below. Since the diagonals bisect each other the top half of the red
diagonal is
= 65. So we label the upper left side 65.
We are given that one of the diagonals is 66. Let that be the red diagonal
below. Since the diagonals bisect each other the top half of the red
diagonal is  of 66 or 33. So we label the top half of the red
diagonal 33. We want to know the length of the green diagonal. So
we label the left half of the green diagonal x.
of 66 or 33. So we label the top half of the red
diagonal 33. We want to know the length of the green diagonal. So
we label the left half of the green diagonal x.
 Since the diagonals of a rhombus are perpendicular, the triangle with
the sides x,33, and 65 is a right triangle, so we can use the Pythagorean
theorem to find x:
x² + 33² = 65²
x² + 1089 = 4225
x² = 3136
x = √3136
x = 56
So half the green diagonal is 56 cm.
Therefore, the whole green diagonal is 2×56 = 112 cm.
Edwin
Since the diagonals of a rhombus are perpendicular, the triangle with
the sides x,33, and 65 is a right triangle, so we can use the Pythagorean
theorem to find x:
x² + 33² = 65²
x² + 1089 = 4225
x² = 3136
x = √3136
x = 56
So half the green diagonal is 56 cm.
Therefore, the whole green diagonal is 2×56 = 112 cm.
Edwin