Question 423336: A liter of orange fruit drink contains 22% orange juice. How many millimeters of orange juice must be added to produce a mixture containing 50% orange juice?
Found 4 solutions by mananth, ikleyn, greenestamps, timofer:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! percent ---------------- quantity
drink 12 ---------------- 1000
juice 100 ---------------- x
Total 50 ---------------- 1000+x
...
12*1000+ 100*x=50 (1000+x)
12000+100x=50000 +50x
100x-50x =50000-12000
50x=38000
/50
x=760 ml
Answer by ikleyn(53521)  (Show Source):
You can put this solution on YOUR website! .
A liter of orange fruit drink contains 22% orange juice. How many millimeters of orange juice
must be added to produce a mixture containing 50% orange juice?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @mananth is irrelevant to the given problem, since it uses
numerical values different from the given input data.
So, I came to provide an adequate solution.
As given, the liter of orange fruit drink contains 22%, or 220 mL of orange juice.
Let assume that we add x milliliters of orange juice.
Then we will have the total volume of 1000 + x milliliters with the (220+x) milliliters
of orange juice.
The concentration will be  .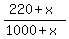
We want this concentration be 50%, or 0.5 as a decimal.
So, our equation is
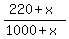= 0.5.
Simplify and find x
220 + x = 0.5 * (1000 + x),
220 + x = 500 + 0.5x,
x - 0.5x = 500 - 220,
0.5x = 280,
x = 280/0.5 = 560.
ANSWER. 560 milliliters of orange juice should be added.
Solved correctly.
Answer by greenestamps(13270)  (Show Source):
You can put this solution on YOUR website!
Any 2-part mixture problem like this can be solved using the following non-algebraic method.
We are mixing 22% juice with 100% juice to obtain a mixture that is 50% juice.
Consider the three percentages 22, 50, and 100 on a number line. The difference between 22 and 50 is 28; the difference between 50 and 100 is 50. That means the two ingredients must be mixed in the ratio 28:50; since 50% is closer to 22% than it is to 100%, the larger portion must be the original liter (1000 ml) of 22% juice.
The problem is then solved using a proportion:
50:28 = 1000:x
1000:560 = 1000:x
ANSWER: 560 ml
Answer by timofer(138)  (Show Source):
|
|
|
