Question 724779: How do you conse log_4 x - 3log_4 2 + log_4 32
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!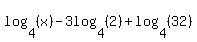 
If these terms were like logarithmic terms then we could add and subtract them. Like logarithmic terms has the same bases and the same arguments. Our logs have the same base, 4, their arguments are different. So we cannot add and subtract them.
Two properties of logarithms,  and , give us another way to combine logarithmic terms. These properties require the same bases and coefficients of 1.
The first and last log of our expression meet both requirements so we could use a property to combine them. But the middle term has a coefficient of 3 (or -3) so it appears that we will not be able to combine it with the other two.
Fortunately there is another property of logarithms,  , which allows us to move the exponent of an argument out in front as a coefficient and vice versa. With this property we can move the coefficient into the argument as its exponent:
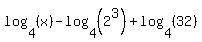
And since 2 cubed is 8:
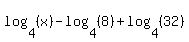
Now that all three logs meet the requirements of the first two properties we can now combine all three. (Two at a time, of course.) To combine the first two logs we will use the second property because its logs, like ours, have a "-" between them:
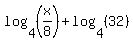
To combine the remaining logs we will use the first property because of the "+" between the logs:
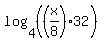
which simplifies to:
This may very well be an acceptable answer.
But there is one more step that could be taken. With a factor of 4 in the argument of a base 4 log, we can simplify this a little more. Using the first property, this time in the other direction (to split the log of a product into the sum of the logs of the factors) we get:
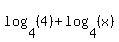
By definition the base 4 log of 4 is 1 so this becomes:
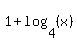
This, or , is the answer to the problem.
|
|
|
