SOLUTION: Greetings I am having trouble with a log problem to solve for X in logx32=5/3 I thought I must change into exponential form and get x^5/3 =2^5 and then go into log form to

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Greetings I am having trouble with a log problem to solve for X in logx32=5/3 I thought I must change into exponential form and get x^5/3 =2^5 and then go into log form to      Log On


   

Question 633354: Greetings I am having trouble with a log problem to solve for X
in logx32=5/3
I thought I must change into exponential form and get x^5/3 =2^5
and then go into log form to get
3/5logx=5log2 and then I am lost.
please help?
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
log%28x%2C+%2832%29%29=5%2F3+
You made a great first step with
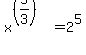
x%5E%28%285%2F3%29%29+=+2%5E5
Not only did you get the variable out of the logarithm, but you recognized that 32+=+2%5E5 which turns out to be a very helpful.

But it's not a good idea to go back to log form. That just puts the x back in the logarithm which is not where we want it. Instead, what we want is to change the exponent on x to a 1. If we can do that, we'll be finished since x%5E1+=+x!

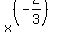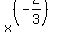So how do we change an exponent? Well there are several rules for exponents that tell us: "When we do __________, we change the exponents in this way.". If we use the multiplication rule (add the exponents) to get an exponent of 1 (by multiplying by x%5E%28%28-2%2F3%29%29 we could get the exponent of 1 on the left but then we would have x%5E%28%28-2%2F3%29%29 on the the right side. If we use the division rule (subtract the exponents) we have a similar problem, We can get the exponent we want on the left but we end up with an x on the right side. The rule that will help us is the power of a power rule (multiply the exponents). If we raise both sides to the right power, we can get an exponent of 1 on the left and there will not be any x's on the right.

So what power to we raise 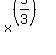x%5E%28%285%2F3%29%29 to to get an exponent of 1? Knowing that we will be multiplying this exponent by 5/3 and knowing that multiplying reciprocals always results in 1, the right power to use is the reciprocal of 5/3: 3/5.
%28x%5E%28%285%2F3%29%29%29%5E%28%283%2F5%29%29+=+%282%5E5%29%5E%28%283%2F5%29%29
On the left, we get the 1 we wanted. On the right, after we multiply 5 and 3/5, we get:
x+=+2%5E3
which simplifies to:
x+=+8

And, as usual with problems where the variable was in the argument or base of a logarithm, we must check the solution to ensure that all arguments and bases of all logarithms remain valid (positive for both and bases cannot be a 1 either). If any argument or base ends up being invalid we must reject that "solution", even if it's the only one we found!

Use the original equation to check:
log%28x%2C+%2832%29%29=5%2F3+
Checking x = 8:
log%28%288%29%2C+%2832%29%29=5%2F3+
We can quickly see that the base is positive (and not a 1) and the argument is positive. So our solution checks!