Question 566479: Solve the following system for (x,y):
1. log9(x)+ logy(8)= 2
2. logx(9)+ log8(y)= (8/3)
The term attached to log is the base, the term in parenthesis the argument. This feels like it should be simple, but after 30 minutes of useless substituting, I figure I'm missing an obvious connection . . .
Thanks to anyone who sees it.
TS
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! I'll connect you.
Let's change variables.
 and 
The first equation transforms easily:
 --> 
For the next one, we have to use a property of logarithms.
As with all the properties of logarithms, you can remember it, or you can rediscover it from the definition of logarithm every time you need it.
I always opted for the second choice, but in this case, rediscovery is not that easy, so I say understand the proof once, and then try to remember that
To help students remember that property, a popular tutor used to call it "skewer it and turn it upside down." That helped because he would write a very large  above the  and pretend it was a toothpick skewering an olive, before pretending to turn it upside down and take it to his mouth, and
the 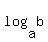 he would then write on the board sort of looks like an upside down . So
 , so  and
 , so 
With that, the second equation gets transformed
 -->  --> 
So we have two equations
and
and just need to find w and z. No logarithm worries (for now).
At this point I would divide the first equation by the second equation
 = -->  --> 
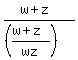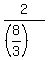If you figure out here that the numbers  and  must be  and  , good for you.
I had to remember that they would be solutions of the quadratic equation
 <-->  and use the quadratic formula.
It could be that  and  ,
or that  and  .
The first solution:
and
-->  --> 
and -->  --> 
The second solution:
and
-->  --> 
-->  --> 
|
|
|
