Question 545054: Find the exact value of the logarithm:
log(base 4)((sqrt4)^(1/4))
Found 2 solutions by josmiceli, bucky:
Answer by josmiceli(19441)   (Show Source):
Answer by bucky(2189)  (Show Source):
You can put this solution on YOUR website! Note that in the explanation of this problem, the numerators of some of the fractions might be clipped off slightly. This is due to the limits of the rendering software that puts things in algebraic form. These numerators are all "1" as you might get from looking at their lower half that does show correctly.
.
You can solve this equation by converting it from the logarithmic form to the exponential form. The rule that applies is, if you are given the logarithmic form:
.
.
You can convert this to the equivalent exponential form:
.
.
This comes from the definition of logarithm as being the exponent that the base must be raised to to give you the quantity that the log operation is operating on.
.
In your problem note that B, the base of the logarithmic operator, is 4.
.
Further, note that the quantity Y that the logarithm is operating on is:
.
.
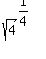
Before proceeding, let's replace the square root operator with its equivalent, an exponent of 
.
This converts Y to the form:
.
.
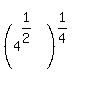
Then by the power rule for exponents, you can multiply 1/2 times 1/4 to get that Y becomes:
.
.
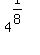
Using that Y has been converted to 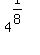and B = 4, we can substitute those two quantities into the exponential form above to get:
.
.
Look carefully at this. Since the base quantity is 4 on both sides, the two exponents have to be equal. Therefore, the unknown exponent E has to equal the exponent E on the right side. So E, the exponent, has to be equal to 
.
That is the answer to this problem. We can return now to the original logarithmic form and substitute for the quantities Y (in its original form given by the problem) and E to have:
.
.
become:
.
.
and from this you can see more clearly that the value of E (that is 1/8) equals the value of the logarithm that you were looking for.
|
|
|
